Chapter: Digital Electronics : Synchronous and Asynchronous Sequential Circuits
Race-Free State Assignment
RACE-FREE STATE ASSIGNMENT
The main objective in choosing a proper binary state assignment is the prevention of critical races.
Critical races are avoided when states between which transitions occur in a flow table are given adjacent assignments. (e.g., 010 and 111 are adjacent).
No critical races can occur in a two-row flow table.
Three-Row Flow Table Example
Consider the following reduced flow-table. For simplicity the outputs have been omitted:
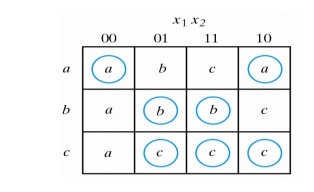
In row a there is a transition from state a to state c and from state a to state c.
This information is transferred into a transition diagram:

The binary state assignment in the transition table will cause a critical race during the transition from a to c because there are two changes in the binary state variables.
A race-free assignment can be obtained by adding an extra row to the flow table:
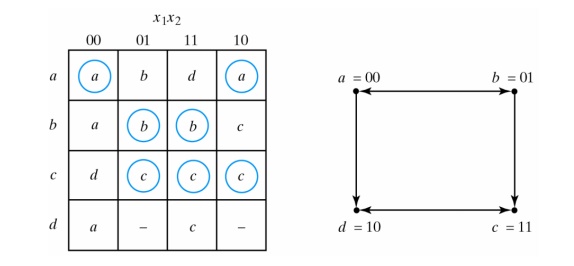
The use of a fourth row does not increase the number of binary state variables, but allows the formation of cycles between two stable states.
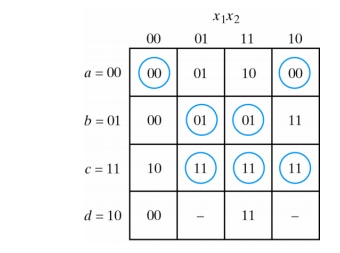
The two dashes represent unspecified states and can be considered don’t care conditions. However, 10 must not be assigned to these squares to avoid an unwanted stable state in the fourth row.
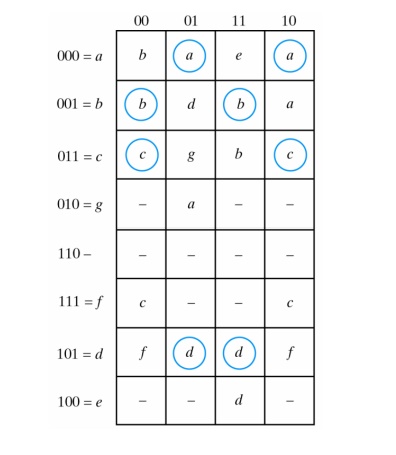
Four-Row Flow Table Example
A flow table with four rows requires a minimum of two state variables.
Consider the following flow table and its corresponding transition diagram:

A state assignment map that is suitable for any four-row flow table is shown below:
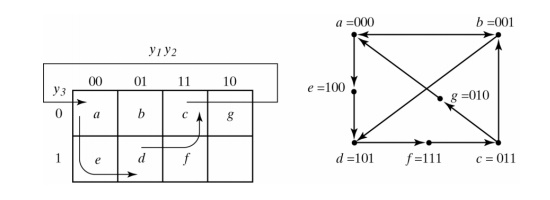
States a, b, c, and d are the original states, and e, f, and g are extra states. The assignment ensures that a cycle is produced so that only one binary variable changes at a time.
By using the assignment given by the map, the four-row table can be expanded to a seven-row table that is free of critical races:
Related Topics