Chapter: Digital Electronics : Synchronous and Asynchronous Sequential Circuits
Analysis Procedure - Asynchronous Sequential Circuits
ANALYSIS PROCEDURE
The analysis of asynchronous sequential circuits proceeds in much the same way as that of clocked synchronous sequential circuits. From a logic diagram, Boolean expressions are written and then transferred into tabular form.
1. Transition Table
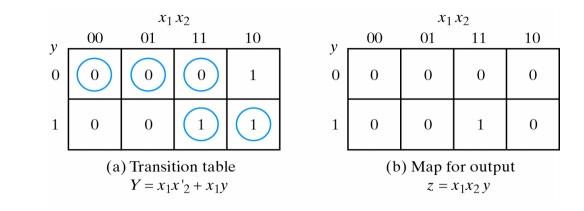
An example of an asynchronous sequential circuit is shown below:
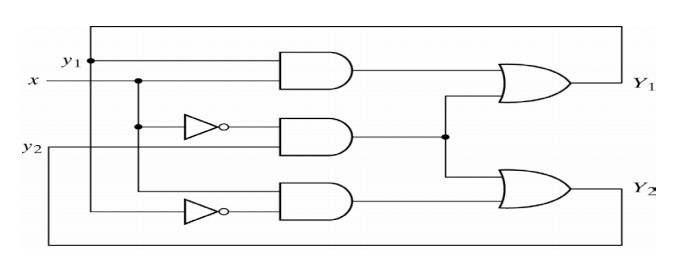
The analysis of the circuit starts by considering the excitation variables (Y1 and Y2) as outputs and the secondary variables (y1 and y2) as inputs.
The next step is to plot the Y1 and Y2 functions in a map:
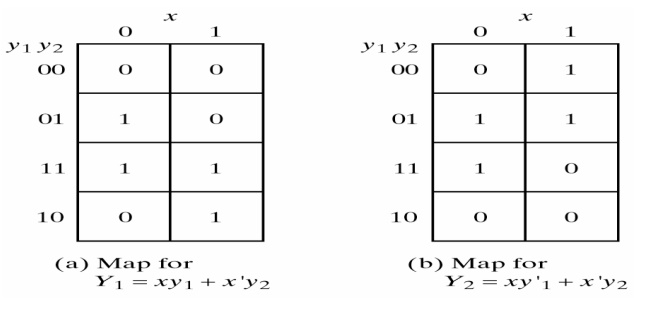
Combining the binary values in corresponding squares the following transition table is obtained:
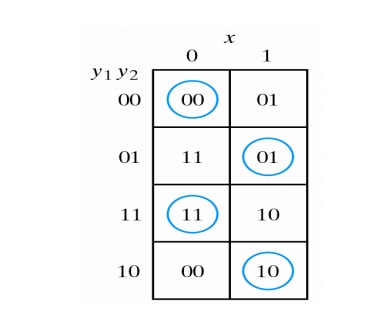
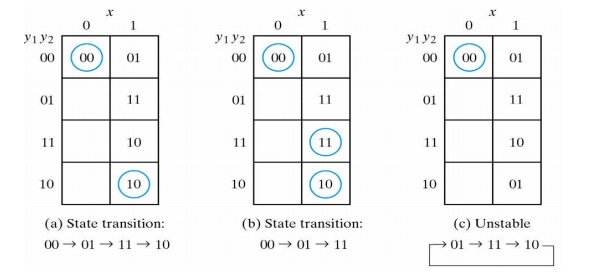
The transition table shows the value of Y = Y1Y2 inside each square. Those entries where Y = y are circled to indicate a stable condition.
The circuit has four stable total states – y1y2x = 000, 011, 110, and 101 – and four unstable total states – 001, 010, 111, and 100.
1. Flow Table
In a flow table the states are named by letter symbols. Examples of flow tables are as follows:
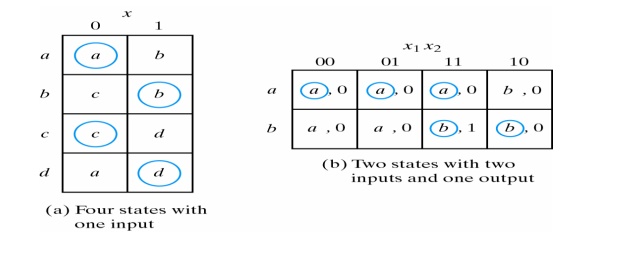
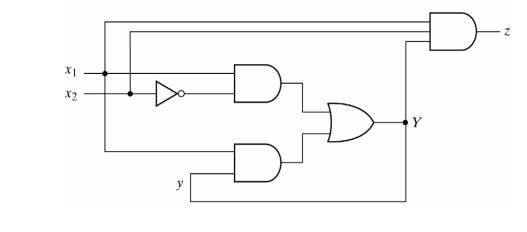
In order to obtain the circuit described by a flow table, it is necessary to assign to each state a distinct value. This assignment converts the flow table into a transition table. This is shown below:
The resulting logic diagram is shown below:
2. Race Conditions
A race condition exists in an asynchronous circuit when two or more binary state variables change value in response to a change in an input variable. When unequal delays are encountered, a race condition may cause the state variable to change in an unpredictable manner.
If the final stable state that the circuit reaches does not depend on the order in which the state variables change, the race is called a non critical race. Examples of non critical races are illustrated in the transition tables below:
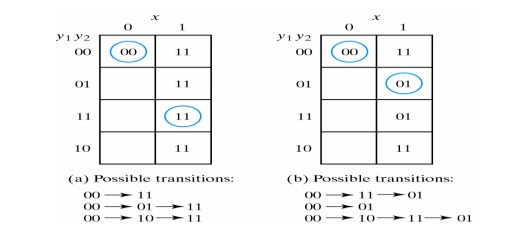
The transition tables below illustrate critical races:
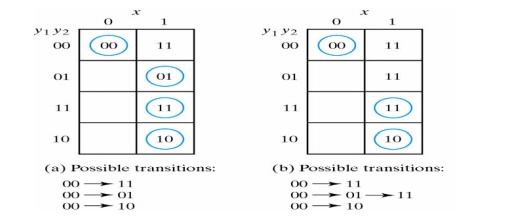
Races can be avoided by directing the circuit through a unique sequence of intermediate unstable states. When a circuit does that, it is said to have a cycle.
Examples of cycles are:
2. ANALYSIS EXAMPLE
Consider the following circuit:
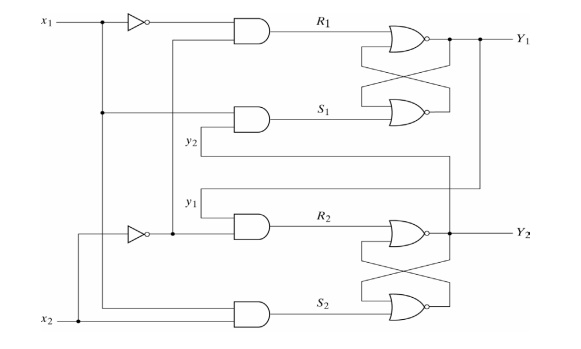
· The first step is to obtain the Boolean functions for the S and R inputs in each latch:
S1 = X1y2 S2 = X1 X2 R1 = X1’X2’ R2 = X2’y1
· The next step is to check if SR = 0 is satisfied:
· The next step is to derive the transition table of the circuit. The excitation functions are derived from the relation Y = S + R′y as:
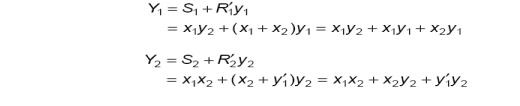
· Next a composite map for Y = Y1Y2 is developed:
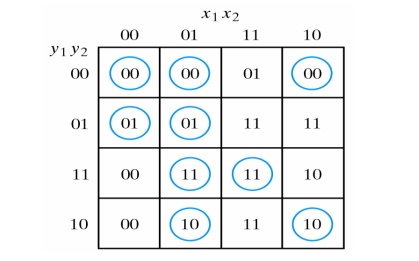
Investigation of the transition table reveals that the circuit is stable. There is a critical race condition when the circuit is initially in total state y1y2x1x2 = 1101 and x2 changes from 1 to 0. If Y1 changes to 0 before Y2, the circuit goes to total state 0100 instead of 0000.
4. DESIGN PROCEDURE
There are a number of steps that must be carried out in order to minimize the circuit complexity and to produce a stable circuit without critical races. Briefly, the design steps are as follows:
1. Obtain a primitive flow table from the given specification.
2. Reduce the flow table by merging rows in the primitive flow table.
3. Assign binary states variables to each row of the reduced flow table to obtain the transition table.
4. Assign output values to the dashes associated with the unstable states to obtain the output maps.
5. Simplify the Boolean functions of the excitation and output variables and draw the logic diagram.
The design process will be demonstrated by going through a specific example:
5. Design Example – Specification
Design a gated latch circuit with two inputs, G (gate) and D (data), and one output Q. The gated latch is a memory element that accepts the value of D when G = 1 and retains this value after G goes to 0. Once G = 0, a change in D does not change the value of the output Q.
Step 1: Primitive Flow Table
A primitive flow table is a flow table with only one stable total state in each row. The total state consists of the internal state combined with the input.
To derive the primitive flow table, first a table with all possible total states in the system is needed:
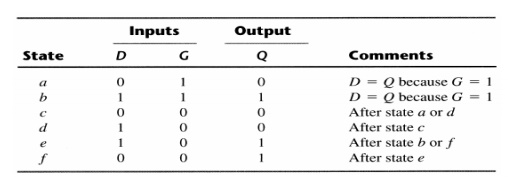
The resulting primitive table for the gated latch is shown below:
First, we fill in one square in each row belonging to the stable state in that row.
Next recalling that both inputs are not allowed to change at the same time, we enter dash marks in each row that differs in two or more variables from the input variables associated with the stable state.
Next we find values for two more squares in each row. The comments listed in the previous table may help in deriving the necessary information. A dash indicates don’t care conditions.
Step 2: Reduction of the Primitive Flow Table
The primitive flow table can be reduced to a smaller number of rows if two or more stable states are placed in the same row of the flow table. The simplified merging rules are as follows:
1. Two or more rows in the primitive flow table can be merged into one if there are nonconflicting states and outputs in each of the columns.
2. Whenever, one state symbol and don’t care entries are encountered in the same column, the state is listed in the merged row.
3. If the state is circled in one of the rows, it is also circled in the merged row.
4. The output state is included with each stable state in the merged row. Now apply these rules to the primitive flow table shown previously.
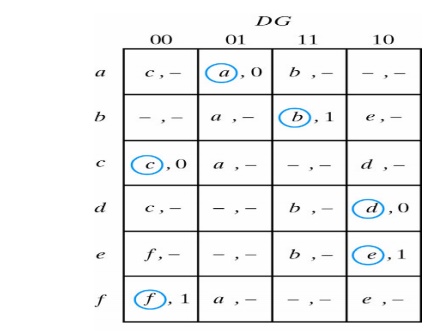
To see how this is done the primitive flow table is separated into two parts of three rows each:
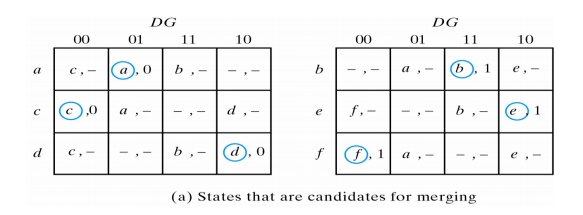
Each part shows three stable states that can be merged because there no conflicting entries in each of the four columns. Since a dash represents a don’t care condition it can be associated with any state or output. The first column of can be merged into a stable state c with output 0, the second into a stable state a with output 0, etc.
The resulting reduced flow table is as follows:

Step 3: Transition Table and Logic Diagram
To obtain the circuit described by the reduced flow table, a binary value must be assigned to each state. This converts the flow table to a transition table.
In assigning binary states, care must be taken to ensure that the circuit will be free of critical races. No critical races can occur in a two-row flow table.
Assigning 0 to state a and 1 to state b in the reduced flow table, the following transition table is obtained:
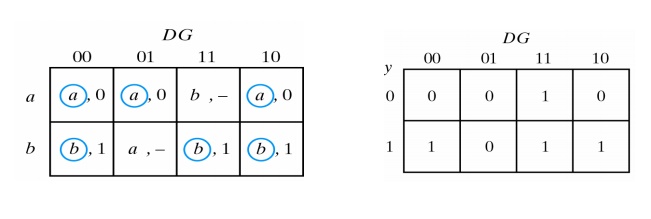
The transition table is, in effect, a map for the excitation variable Y. The simplified Boolean function for Y as obtained from the map is:
Y = DG +G′’y
There are two don’t care outputs in the final reduced flow table. By assigning values to the output as shown below:
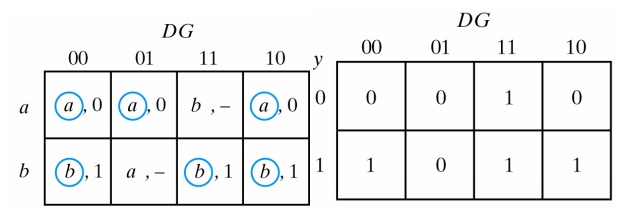
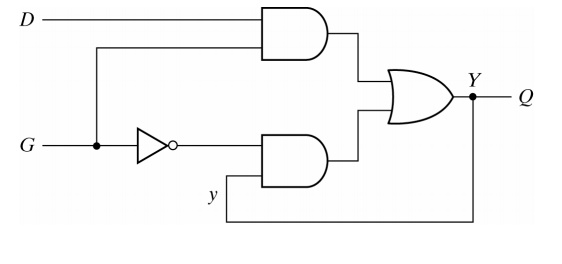
It is possible to make output Q equal to Y. If the other possible values are assigned to the don’t care outputs, output Q is made equal to y. In either case, the logic diagram of the gated latch is as follows:
6. REDUCTION OF STATE AND FLOW TABLES
The procedure for reducing the number of internal states in an asynchronous sequential circuit resembles the procedure that is used for synchronous circuits.
7. Implication Table
The state-reduction procedure for completely specified state tables is based on the algorithm that two states in a state table can be combined into one if they can be shown to be equivalent.
There are occasions when a pair of states do not have the same next states, but, nonetheless, go to equivalent next states.
Consider the following state table:

(a, b) imply (c, d) and (c, d) imply (a, b). Both pairs of states are equivalent; i.e., a and b are equivalent as well as c and d.
The checking of each pair of states for possible equivalence in a table with a large number of states can be done systematically by means of an implication table. This a chart that consists of squares, one for every possible pair of states, that provide spaces for listing any possible implied states.
Consider the following state table:
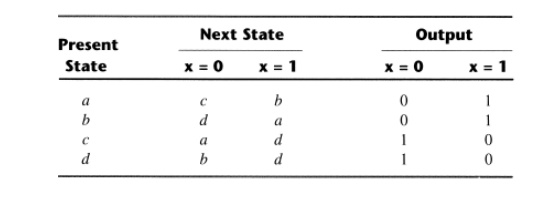
The implication table is:
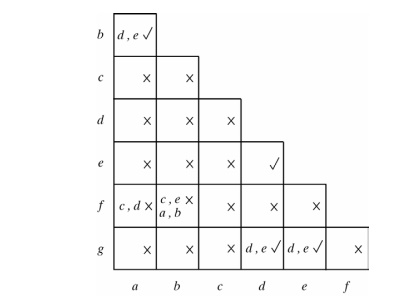
On the left side along the vertical are listed all the states defined in the state table except the last, and across the bottom horizontally are listed all the states except the last.
The states that are not equivalent are marked with a ‘x’ in the corresponding square, whereas their equivalence is recorded with a ‘√’.
Some of the squares have entries of implied states that must be further investigated to determine whether they are equivalent or not.
The step-by-step procedure of filling in the squares is as follows:
1. Place a cross in any square corresponding to a pair of states whose outputs are not equal for every input.
2. Enter in the remaining squares the pairs of states that are implied by the pair of states representing the squares. We do that by starting from the top square in the left column and going down and then proceeding with the next column to the right.
3. Make successive passes through the table to determine whether any additional squares should be marked with a ‘x’. A square in the table is crossed out if it contains at least one implied pair that is not equivalent.
4. Finally, all the squares that have no crosses are recorded with check marks. The equivalent states are: (a, b), (d, e), (d, g), (e, g).
We now combine pairs of states into larger groups of equivalent states. The last three pairs can be combined into a set of three equivalent states (d, e, g) because each one of the states in the group is equivalent to the other two. The final partition of these states consists of the equivalent states found from the implication table, together with all the remaining states in the state table that are not equivalent to any other state:
(a, b) (c) (d, e, g) (f)
The reduced state table is:

8. Merging of the Flow Table
There are occasions when the state table for a sequential circuit is incompletely specified.
Incompletely specified states can be combined to reduce the number of states in the flow table. Such states cannot be called equivalent,
but, instead they are said to be compatible.
The process that must be applied in order to find a suitable group of compatibles for the purpose of merging a flow table is divided into three steps:
1. Determine all compatible pairs by using the implication table.
2. Find the maximal compatibles using a merger diagram.
3. Find a minimal collection of compatibles that covers all the states and is closed.
We will now proceed to show and explain the three procedural steps using the following primitive flow table:
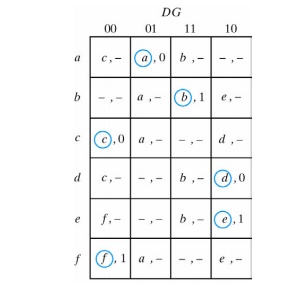
9. Compatible Pairs
Two states are compatible if in every column of the corresponding rows in the flow table, they are identical or compatible states and if there is no conflict in the output values.
The compatible pairs (√) are:
(a, b) (a, c) (a, d) (b, e) (b, f) (c, d) (e, f)
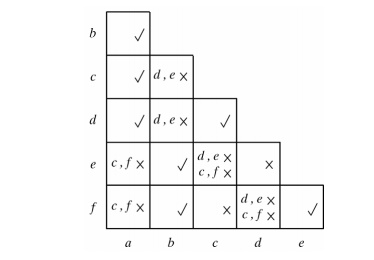
10. Maximal Compatibles
The maximal compatible is a group of compatibles that contains all the possible combinations of compatible states. The maximal compatible can be obtained from a merger diagram:
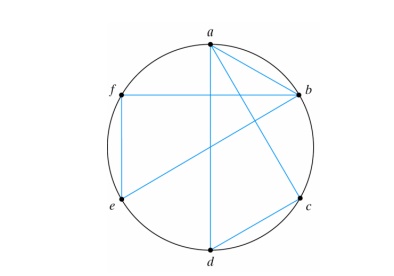
The above merger diagram is obtained from the list of compatible pairs derived from the previous implication table. A line represents a compatible pair. A triangle constitutes a compatible with three states. The maximal compatibles are:
(a, b) (a, c, d) (b, e, f)
In the case where a state is not compatible to any other state, an isolated dot represents this state.
Related Topics