with Answer, Solution, Formula - Second Order first degree differential equations with constant coefficients: Solved Example Problems | 12th Business Maths and Statistics : Chapter 4 : Differential Equations
Chapter: 12th Business Maths and Statistics : Chapter 4 : Differential Equations
Second Order first degree differential equations with constant coefficients: Solved Example Problems
Example 4.25
Solve (D 2 −
3D − 4)y = 0
Solution:
Given (D 2
− 3D − 4)y = 0
The auxiliary equations is
m2 − 3m − 4 = 0
( m − 4)( m + 1) = 0
m = −1,
4
Roots are real and different
∴ The complementary
function is Ae−x + Be4 x
The general solution is y = Ae−x + Be4 x
Example 4.26
Solve 9 y ′′ − 12 y′ + 4 y =
0
Solution:
Given ( 9D2
− 12D + 4) y = 0
The auxiliary equation is
( 3m – 2)2 = 0
(3m – 2) ( 3m – 2) =
0 ⇒ m =
2/3,2/3
Roots are real and equal
The C.F. is (
Ax + B )e 2x/3
The general solution is y = ( Ax +
B )e 2x/3


Type II : f ( x ) = e ax (i.e ) f( D ) y = eax


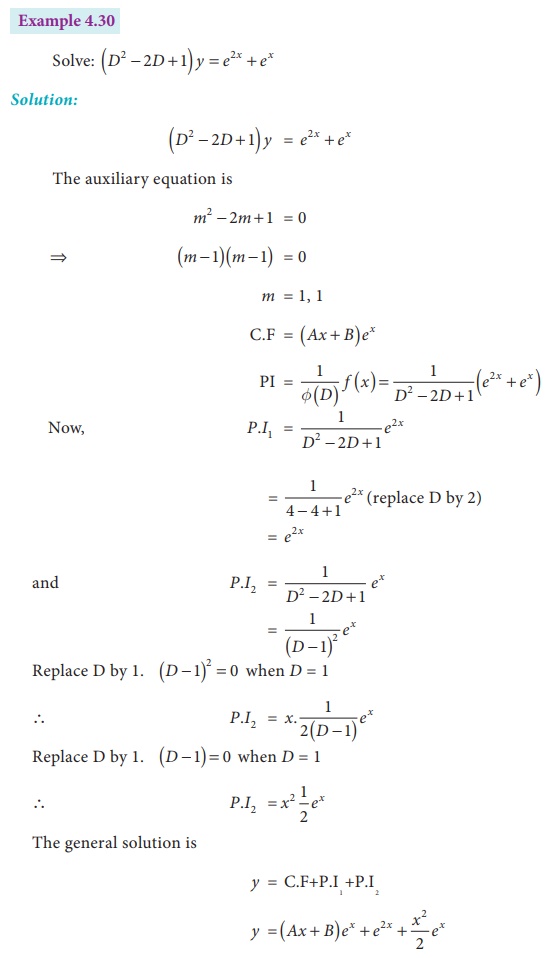


Example 4.32
Suppose that the quantity demanded Qd = 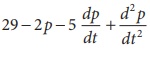 and quantity supplied Qs = 5 + 4 p where p is the price. Find the
equilibrium price for market clearance.
and quantity supplied Qs = 5 + 4 p where p is the price. Find the
equilibrium price for market clearance.
Solution:
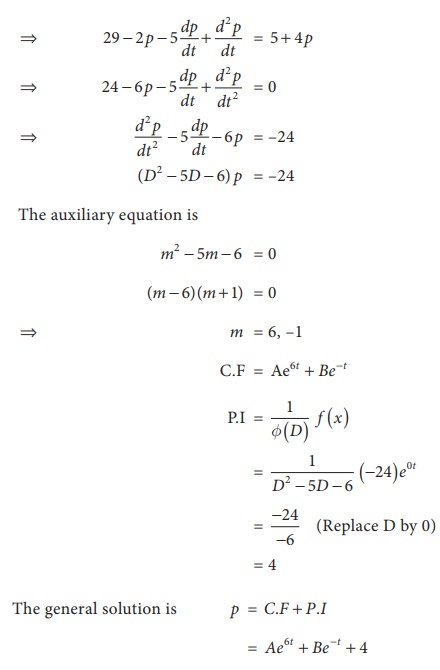
Related Topics