Linear differential equations of first order

Linear differential equations of first order:

A differential equation is said to be linear when the dependent variable and its derivatives occur only in the first degree and no product of these occur.

The most general form of a linear equation of the first order is dy/dx + Py = Q (1)

P and Q are functions of x alone.

Equation (1) is linear in y. The solution is given by ye^{∫ pdx} = ∫Qe^{∫ pdx}dx + c . Here e^{∫ pdx} is known as an integrating factor and is denoted by I.F.

Example

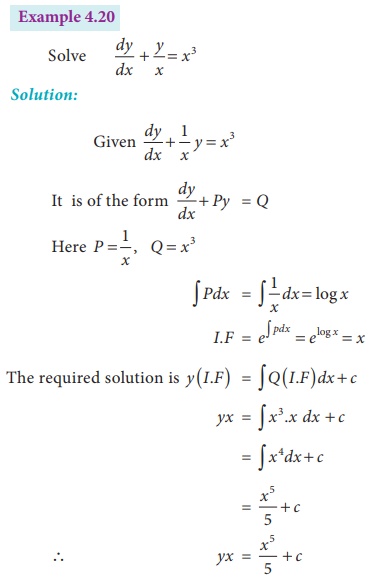
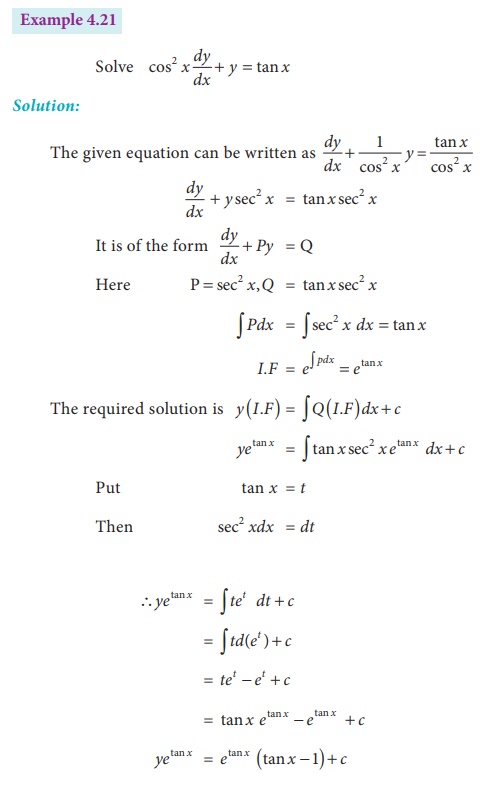
Example 4.24

A firm has found that the cost C of producing x tons of certain product by the equation x dC/dx = 3/x − C and C = 2 when x = 1. Find the relationship between C and x.

Solution: