Homogeneous Differential Equations

Homogeneous Differential Equations

A differential equation of the form dy/dx = f (x, y)/ g (x, y) is called homogeneous differential equation if f (x, y) and g(x, y) are homogeneous functions of the same degree in x and y. (or)

Homogeneous differential can be written as dy/dx = F(y/x).

Method of solving first order Homogeneous differential equation

Check f ( x, y) and g ( x, y) are homogeneous functions of same degree.

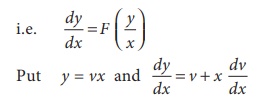
The given differential equation becomes v x dv/dx =F(v)

Separating the variables, we get

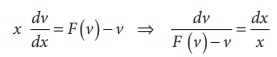
By integrating we get the solution in terms of v and x.

Replacing v by y/x  we get the solution.

Example 4.15

Solve the differential equation y² dx + ( xy + x² )dy = 0

Solution

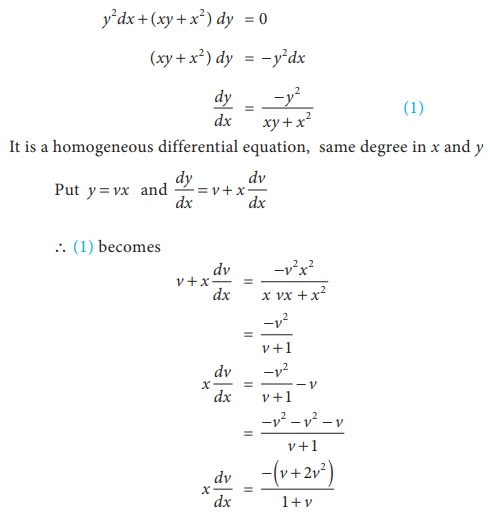
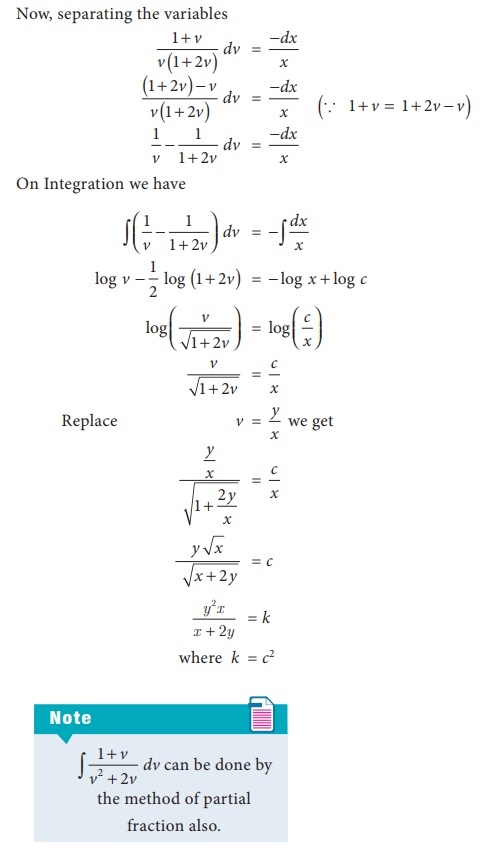
Example 4.17

Find the particular solution of the differential equation x ² dy + y ( x + y) dx = 0 given that x = 1, y = 1

Solution:

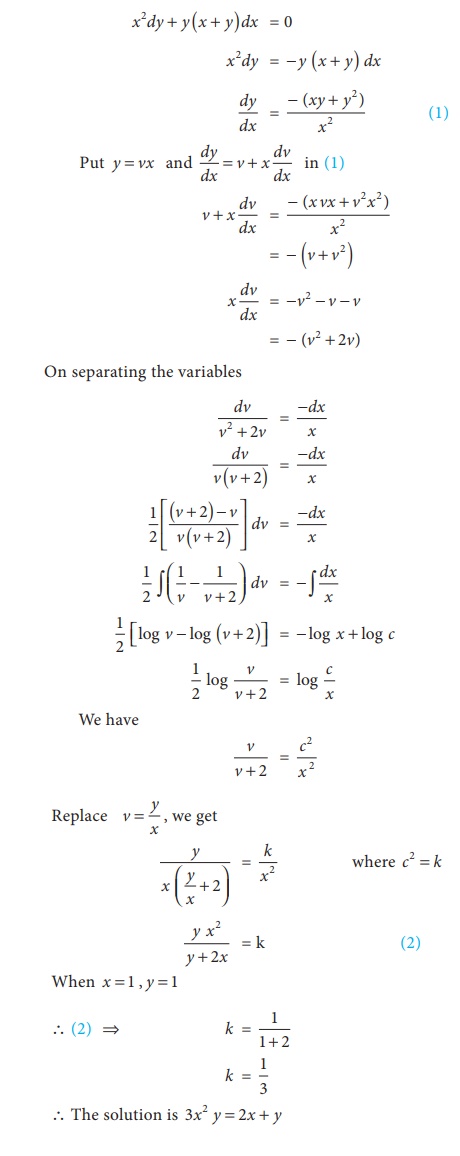
Example 4.18

If the marginal cost of producing x shoes is given by (3xy + y² ) dx + (x ² + xy) dy = 0 and the total cost of producing a pair of shoes is given by ₹12. Then find the total cost function.

Solution:

Given marginal cost function is (x² + xy) dy + (3xy + y²)dx=0

Example 4.19

The marginal revenue ‘y’ of output ‘q’ is given by the equation 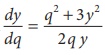. Find the total Revenue function when output is 1 unit and Revenue is ₹5.

Solution: