First order and first degree differential

First order and first degree differential

A differential equation of first order and first degree can be written as f( x, y, dy/dx) = 0.

Here we will discuss the solution of few types of

General solution and particular solution

For any differential equations it is possible to find the general solution and particular solution.

Differential Equation in which variables are separable

If in an equation it is possible to collect all the terms of x and dx on one side and all the terms of y and dy on the other side, then the variables are said to be separable. Thus the general form of such an equation is

f(x)dx = g(y)dy (or) f(x)dx + g(y)dy = 0

By direct integration we get the solution.

Example 4.6

Solve: ( x² + x +1) dx + ( y² - y + 3)dy  = 0

Solution:

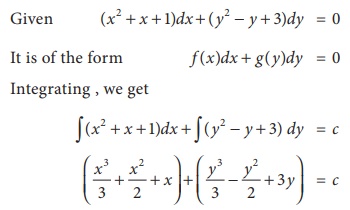
Example 4.12

The marginal cost function of manufacturing x gloves is 6 + 10x − 6x² . The total cost of producing a pair of gloves is ₹100. Find the total and average cost function.    

Solution:

Example 4.13

The normal lines to a given curve at each point ( x, y) on the curve pass through the point (1,0). The curve passes through the point (1,2). Formulate the differential equation representing the problem and hence find the equation of the curve.

Solution:

Example 4.14

The sum of ₹2,000 is compounded continuously, the nominal rate of interest being 5% per annum. In how many years will the amount be double the original principal? (log_e 2 = 0.6931)

Solution: