Example Solved Problems with Answer, Solution, Formula - Order and degree of a differential equation | 12th Business Maths and Statistics : Chapter 4 : Differential Equations
Chapter: 12th Business Maths and Statistics : Chapter 4 : Differential Equations
Order and degree of a differential equation
Order and degree of a differential equation
The highest order derivative present in the differential equation
is the order of the differential equation.
Degree is the highest power of the highest order derivative in the
differential equation, after the equation has been cleared from fractions and
the radicals as for as the derivatives are concerned.
For example, consider the differential equation
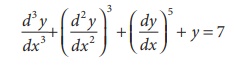
Here the highest order derivatives is 
( i.e 3rd order
derivative). So the order of the differential equation is 3.
Now the power of highest order derivative is 1.
∴ The degree of the differential equation is 1.
Example 4.1
Find the order and degree of the following differential equations.
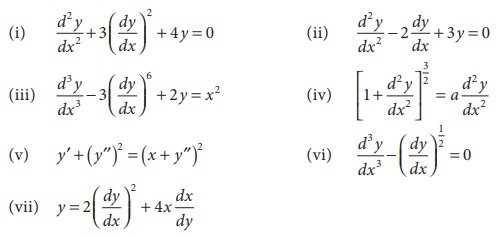
Solution
Family of Curves
Sometimes a family of curves can be represented by a single
equation with one or more arbitrary constants. By assigning different values
for constants, we get a family of curves. The arbitrary constants are called
the parameters of the family.
For example,
(i) y 2
= 4ax represents
the equation of a family of parabolas having the origin as vertex where
‘a’ is the parameter.
(ii) x 2 + y2 = a2 represents the equation of family of circles having the origin as
centre, where ‘a’ is the parameter.
(iii) y = mx + c represents the equation
of a family of straight lines in a plane, where m and c are parameters.
Related Topics