A general second order linear differential equation with constant coefficients is of the form

Second Order first degree differential equations with constant coefficients 

A general second order linear differential equation with constant coefficients is of the form

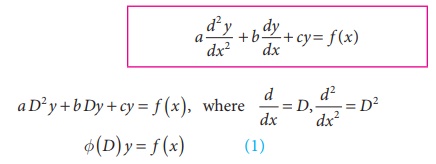
where ϕ(D) = aD² + bD + c (a,b and c are constants)

To solve the equation (1), we first solve the equation ϕ ( D ) y = 0. The solution so obtained is called complementary function (C.F).

Next we operate on f ( x) with 1/ ϕ ( D) , the solution so obtained is called particular integral (P.I)

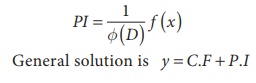
Type 1 : f(x) = 0

(i.e) ϕ(D)y = 0

To solve this, put ϕ ( D) = 0

Replace D by m. This equation is called auxiliary equation . ϕ( m ) = 0 is a quadratic equation. So we have two roots, say m₁ and m₂.

Now we have the following three cases

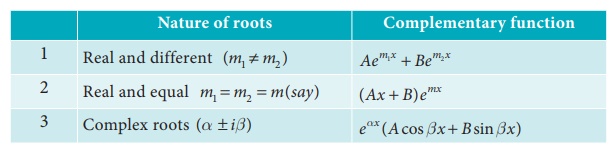
Here A and B are arbitrary constants