Example Solved Problems with Answer, Solution, Formula - Formation of ordinary differential equation | 12th Business Maths and Statistics : Chapter 4 : Differential Equations
Chapter: 12th Business Maths and Statistics : Chapter 4 : Differential Equations
Formation of ordinary differential equation
Formation of ordinary differential equation:
Consider the equation f (
x, y ,c1 )
= 0 -------(1) where c1
is the arbitrary constant. We form the differential equation from this
equation. For this, differentiate equation (1) with respect to the independent
variable occur in the equation.
Eliminate the arbitrary constant c from (1) and its
derivative. Then we get the required differential equation.
Suppose we have f (
x, y ,c1 ,c2 ) = 0 . Here we have two
arbitrary constants c1 and c2 . So, find
the first two successive derivatives. Eliminate c1 and c2
from the given function and the successive derivatives. We get the required
differential equation.
Note
The order of the differential equation to be formed is equal to
the number of arbitrary constants present in the equation of the family of
curves.
Example 4.2
Find the differential equation of the family of straight lines y=mx+cwhen
(i) m is the arbitrary constant (ii) c is the arbitrary constant (iii) m and c both are arbitrary
constants.
Solution:

Example 4.3
Find the differential equation of the family of curves y= a/x + b
where a and b are arbitrary constants.
Solution:

Example 4.4
Find the differential equation corresponding to y = ae4x
+ be−x where a, b are arbitrary constants,
Solution:

Example 4.5
Find the differential equation of the family of curves y = ex ( a cos x + b sin x) where a and b
are arbitrary constants.
Solution :
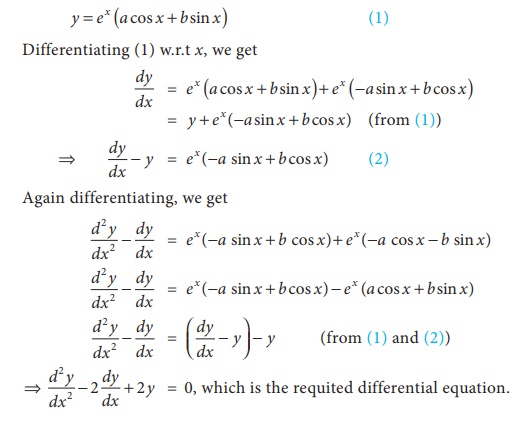
Related Topics