Sampling Statistics

SAMPLING STATISTICS

The errors that are solely attributed to sampling, specifically in the instance of heterogeneous solids, usually give rise to the most important source of uncertainty in carrying out analysis of pharma-ceutical substances.

Thus, the overall standard deviation, s_T, i.e., the total error is given by the following expression :

              ......................(i)

where, S_S = Standard deviation of the sampling procedure (i.e., the sampling error), and S_A = Standard deviation of the analytical procedures (i.e., the analytical error).

The Eq. (i) may also be expressed as :

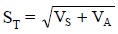
where  V_S = Variance due to sampling, and

V_A = Variance due to analytical method(s).

The individual determination of V_S and V_A may be accomplished by using the method described under variance.

Example : If the sampling error is ± 2.8% and the analytical errors by two different analysts come out to be ± 0.9% and ± 0.1% respectively, we may have :

From Eqs. (a) and (b) it is quite evident that the actual contribution of the analytical error viz., ± 0.9% and ± 0.1%, to the total error (S _T) is more or less insignificant.

Note : Youden* (1967) suggested that once the analytical error is reduced to 1/3rd of the sampling error, further reduction of the former is not required anymore.

In order to have a meaningful ‘sampling plan’ the following points should be taken into consideration**, namely :

·              Number of samples to be taken :

·              Size of the sample, and

·              Should separate samples be analysed or should a sample made up of two or more increments (i.e., composite sample) be prepared.

Unknown Bulk Material : 

A container-load of Paracetamol (10 MT) arrives at a raw-material stores and the composition of the bulk material is unknown, it will be a sensible and logical practice to carry out first and foremost a preliminary investigation by collecting a large number of samples and assaying the analyte of interest.

Thus, the confidence limits are given by the following expression :

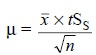           ............................(c)

where,      µ = Estimate of the true mean,

 x’ = Mean of the analytical results,

t = Parameter depending upon the number of degrees of freedom (ν) and the confidence level required,

S_S = Standard deviation of individual sample, and

n = Number of samples taken.

Example : The estimate in variability of Paracetamol in a consignment of 10 MT, based on 20 determinations, was found to be ± 1.4%. How many samples must be taken to give (at 95% confidence level) a sampling error of less than 0.5% paracetamol ?

The 0.5% value, in reality, represents the difference between the sample mean x and the actual value µ. If this value is designated by E, then Eq. (c) may be expressed as :

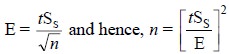
From the tables [Percentage Points of the t-Distribution] the value of t for (n – 1 ), 19 degrees of freedom at 95% confidence level is 2.09.

Conclusion : 

From this test it has been established that at least 34 samples are required if the specifi-cations provided in the above cited example are to be fulfilled adequately.

Sample Size : 

Another major problem associated with the sampling process is that of the sample size.

In fact, the sample size withdrawn from a heterogeneous material is solely guided by two factors, namely :

(a) Variation in particle size, and

(b) Precision required in the results of the analysis.

The sampling variance, V, is inversely proportional to the actual number of sampling increments (n) and may be expressed as :

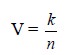
where,  k = Constant entirely dependent on the size of the increment and variation within the bulk material.

The following points with regard to sampling may be observed carefully :

·              A major source of error in sampling may be incorporated from the actual process of taking increments from the bulk material,

·              The accuracy of the sample is determined by its total size (based on Random Sampling Theory), and

·              The number of increments taken shall directly influence the sampling accuracy provided the bulk material comprises of varying particle sizes.