Classification of Errors in Pharmaceutical Analysis

CLASSIFICATION OF ERRORS

The numerous uncertainties usually encountered in a chemical analysis give rise to a host of ‘errors’ that may be broadly categorised into two heads, namely :

(i) Determinate (systematic) Errors, and

(ii) Indeterminate (random) Errors.

It is pertinent to mention here that it becomes rather difficult at times to place a particular ‘error’ into one of the above mentioned categories ; however, the classification may prove to be beneficial with regard to study of the various analytical errors that crop up in the course of routine analysis.

1. DETERMINATE (SYSTEMATIC) ERRORS

These are errors that possess a definite value together with a reasonable assignable cause; however, in principle these avoidable errors may be measured and accounted for coveniently. The most important errors belonging to this particular class are :

(a) Personal Errors : They are exclusively caused due to ‘personal equation’ of an analyst and have no bearing whatsoever either on the prescribed procedure or methodology involved.

(b) Instrumental Errors : These are invariably caused due to faulty and uncalibrated instruments, such as : pH meters, single pan electric balances, uv-spectrophotometers, potentiometers etc.

(c) Reagent Errors : The errors that are solely introduced by virtue of the individual reagents, for instance : impurities inherently present in reagents ; high temperature volatalization of platinum (Pt) ; unwanted introduction of ‘foreign substances’ caused by the action of reagents on either porcelain or glass apparatus.

(d) Constant Errors : They are observed to be rather independent of the magnitude of the measured amount ; and turn out to be relatively less significant as the magnitude enhances.

Example : Assuming a constant equivalence—point error of 0.10 ml is introduced in a series of titrations, hence for a specific titration needing only 10.0 ml of titrant shall represent a relative error of 1% and only 0.2% for a corresponding 50 ml of titrant consumed.

(e) Proportional Errors : The absolute value of this kind of error changes with the size of the sample in such a fashion that the relative error remains constant. It is usually incorporated by a material that directly interferes in an analytical procedure.

Example : Estimation of ‘chlorate’—an oxidant by iodometric determination. In this particular instance two things may happen, namely :

(i) Presence of ‘Bromate’—another oxidizing agent would give rise to positively higher results, and hence, it must be duly corrected for, and

(ii) Absolute error might increase while dealing with large samples, whereas the relative error would remain more or less constant if the sample is perfectly homogenous,

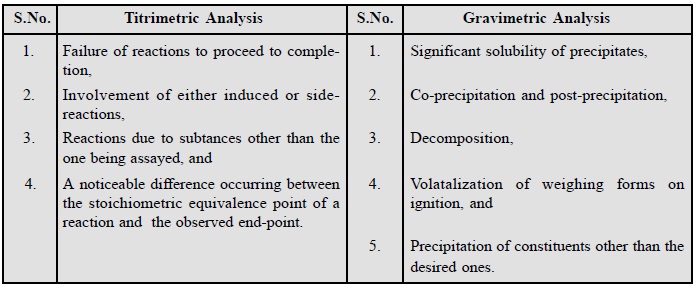
(f) Errors due to Methodology : Both improper (incorrect) sampling and incompleteness of a reaction often lead to serious errors. A few typical examples invariably encountered in titrimetric and gravimetric analysis are cited below :

(g) Additive Errors : It has been observed that the additive errors are independent of the quantum of the substances actually present in the assay.

Examples : (i) Errors caused due to weights, and

(ii) Loss in weight of a crucible in which a precipitate is incenerated.

Detection of this error is ascertained by taking samples of different weights.

2. INDETERMINATE (RANDOM) ERRORS

As the name suggests, indeterminate errors cannot be pin-pointed to any specific well-defined reasons. They are usually manifested due to the minute variations which take place inadvertently in several successive measurements performed by the same analyst, using utmost care, under almost identical experimental parameters. These errors are mostly random in nature and ultimately give rise to high as well as low results with equal probability. They can neither be corrected nor eliminated, and therefore, form the ‘ultimate limitation’ on the specific measurements. It has been observed that by performing repeated measurement of the same variable, the subsequent statistical treatment of the results would have a positive impact of ‘reducing their importance’ to a considerable extent.

Example : Figure 3.1, represents the absolute errors in nitrogen analysis by means of micro Kjeldahl’s Method*. Here, each vertical line labelled ( x’₁ – x_t) designates the absolute deviation of the mean of the set from the true value. In Figure 3.1, A represents ( x’₁ – x_t) the absolute error obtained by ‘analyst-1’ for the assay of benzyl-iso-thioureahydrochloride, whereas B represents ( x’₂ – x_t) the absolute error obtained by ‘analyst-2’ for the assay of the same compound.

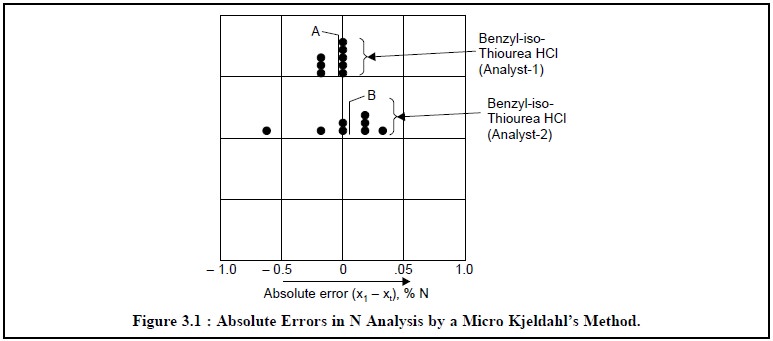
Thus, it is evident from Figure 3.1, that the broad spread of individual errors centres around the mean values (x’_n – x ) thereby affording a direct indication of indeterminate type uncertainties. Hence, larger indeterminate errors seem to be linked with the performance of ‘analyst-2’ than with that of ‘analyst-1’.

Salient Features of Indeterminate Errors

The various salient features of indeterminate errors are enumerated below :

1)          Repeated mesurement of the same variable several times and subsequent refinement to the extent where it is simply a coincidence if the corresponding replicates eventually agree to the last digit,

2)          Both unpredictable and imperceptible factors are unavoidably incorporated in the results what generally appear to be ‘random fluctuations’ in the measured quantity,

3)          Recognition of specific definite variables which are beyond anyone’s control lying very close to the performance limit of an instrument, such as : temperature variations, noise as well as drift from an electronic circuit, and vibrations caused to a building by heavy vehicular-traffic,

4)          A variation that may be regarded as random by a slipshod analyst may at the same time prove to be quite evident and manageable by a careful observer, and

5)          The average of a number of fine observations having random scatter is definitely more accurate, precise and, hence, more cogent than coarse data that appear to agree perfectly.

3. ACCURACY

In connexion with the scientific data the two terminologies ‘accuracy’ and ‘precision’ are invariably practised synonymously, but there exists a clear distinction between them as discussed below :

In usual practice an accurate result is the one which matches very nearly with true value of a measured amount. The comparison is normally done with regard to the ‘error’; and the accuracy is inversely propor-tional to it i.e., the greater the accuracy, the smaller is the error. ‘Absolute error’ is the difference between the experimental value and the true value.

Example : An analyst determines a value of 70.55% cineole in a fresh sample of Eucalyptus Oil that actually contains 70.25%, the absolute error is given by :

70.55 – 70.25 = 0.30%

The error thus obtained is invariably stated with regard to the actual size of the measured quantity i.e., either in percent (%) or in parts per thousand (ppt). Therefore, the relative error is given by :

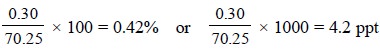
4. PRECISION

It may be defined as—‘the agreement amongst a cluster of experimental results ; however, it does not imply anything with respect to their relation to the ‘true value’ ’. Precision designates ‘reproducibility’ of a measurement, whereas accuracy the correctness of a measurement. Precision invariably forms an integral part of accuracy, but ironically a high degree of precision may not necessarily suggest accuracy.

Example : A sample of pure Peppermint Oil is known to contain 30.10 ± 0.03 per cent of Menthone. The results obtained by two Analysts-1 and 2 employing the same sample of peppermint oil and making use of the same analytical reagents and procedure are as stated below :

The arithmetic mean is 31.44% and the results vary between 31.40% to 31.46%

The ultimate results of the analysis put forward by the Analysts-1 and 2 may be summarized as under :

(i) The results achieved by Analyst-1 are fairly accurate i.e., in close proximity to the correct result ; however, the precision stands at an inferior level to the results obtained by Analyst-2. The results accomplished by Analyst-2 are indeed extremely precise but fail in accuracy,

(ii) The results of Analyst-1 lie on either sides of the average value as shown by two ‘cross-signs’ on each side which might have been caused due to ‘random errors’ discussed earlier. It is quite evi-dent that there exists a constant (determinate) error in the results obtained by the Analyst-2, and

(iii) In case, Analyst-3 had performed the estimations on the very same day in quick succession i.e., one after the other, this type of analysis could be termed as ‘repeatable analysis’. If the estimations had been carried out on two separate days altogether, thereby facing different laboratory conditions then the results so obtained would be known as ‘reproducible analysis’.

In short, there exists a marked and pronounced distinction between a within-run precision (i.e., repeatability) and an in-between-run precision (i.e., reproducibility).

5. MINIMISING SYSTEMATIC ERRORS

Systematic errors may be reduced substantially and significantly by adopting one of the following procedures rigidly, such as :

(i) Calibration of Instruments, Apparatus and Applying Necessary Corections

Most of the instruments, commonly used in an analytical laboratory, such as : UV-Spectrophoto-meter, IR-Spectrophotometer, single—pan electric balance, pH-meter, turbidimeter and nephelometer, polarimeter, refractometer and the like must be calibrated duly, before use so as to eliminate any possible errors. In the same manner all apparatus, namely : pipettes, burettes, volu-metric flasks, thermometers, weights etc., must be calibrated duly, and the necessary corrections incorporated to the original measurements

In some specific instances where an error just cannot be avoided it may be convenient to enforce an appropriate correction for the effect that it ultimately causes ; for instance : the inherent impu-rity present in a weighed precipitate can be estimated first and then deducted duly from its weight.

(ii) Performing a Parallel Control Determination

It essentially comprises of performing an altogether separate estimation under almost identical experimental parameters with a quantity of a standard substance that consists of exactly the same weight of the component as is present in the unknown sample. Thus, the weight of the component present in the unknown sample may be calculated with the help of the following expression :

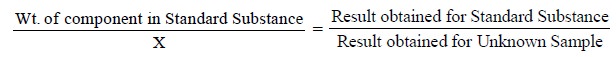
where,             X = Weight of the component present in the Unknown Sample.

Note :             A good number of Standard Samples, including primary standards, such as : arsenic trioxide, benzoic acid, potassium hydrogen phthalate, sodium oxalate, are available as :

BPCRS = British Pharmacopoeia Chemical Reference Substance,

EPCRS = European Pharmacopoeia Chemical Reference Substance,

CRM = BCS—Certified Reference Materials,

ECRM = EURONORM—Certified Reference Materials.

(iii) Blank Determination :

In order to ascertain the effect of the impurities present in the reagents employed and reaction vessels used ; besides establishing exactly the extent to which an excess of standard solution required to locate the exact end-point under the prevailing experimental parameters of the unknown sample—a blank determination is an absolute necessity. It may be accomplished by performing a separate parallel estimation, without using the sample at all, and under identical experimental parmeters as employed in the actual analysis of the given sample.

Note : Always avoid using an appreciably large blank correction which gives rise to a vague and uncertain ‘exact value’ thereby minimising the precision of the analysis.

(iv) Cross-checking Results by Different Methods of Analysis

In certain specific cases tha accuracy of a result may be cross-checked by performing another analysis of the same substance by an altogether radically different method.

Examples :

(a) HCl-Solution : It may be assayed either by titration with a standard solution of a strong alkali (NaOH), or by precipitation and weighing as AgCl ; and

(b) Fe³⁺ : It may be assayed either by gravimetric method as Fe(III) hydroxide after getting rid of the interfering elements and igniting the precipitate to Fe(III) oxide, or by titrimetric method i.e., first reducing to the Fe(II) state and then titrating with a suitable oxidizing agent, for instance Ce(IV) sulphate, K₂Cr₂O₇. In short, the results thus obtained by the two fundamen-tally different techniques must be concordant thereby justifying and ascertaining the fact that the values obtained are fairly small limits of error.

(v) Method of Standard Addition

Here, a small known quantity of the component under estimation is added to the sample, which is subsequently subjected to analysis for the total amount of component present. The actual differ-ence in the quantity of components present in samples with or without the added component ultimately gives the recovery of the quantum added component. A good satisfactory recovery builds up the confidence in the accuracy of the method of analysis.

Note : The method of ‘standard addition’ is particularly useful to physicochemical techniques

of analysis, for instance : spectrophotometry, turbidimetry.

(vi) Method of Internal Standards

The specific method is of immense value both in chromatographic as well as spectroscopic determinations. Here, a fixed quantity of a reference substance (i.e., the ‘internal standard’) is added to a series of known concentrations of the material to be assayed.

A graph is plotted between the concentration values and the ratios obtained from the physical value (i.e., peak area of absorption) of the ‘internal standard’ and the series of known concentra-tions, thereby producing a straight line. Any unknown concentration may be determined effec-tively by adding the same amount of ‘internal standard’ and locating exactly where the ratio obtained falls on the concentration scale.