Statistical Treatment of Finite Samples

STATISTICAL TREATMENT OF FINITE SAMPLES

The various techniques by which one may effectively treat the scientific data normally obtained in actual analytical procedures are enumerated below :

1. Mean

It is the average of a series of results. The mean of a finite number of measurements, x_l, x₂, x₃, x₄, ........, x_n, is commonly represented as x’. It may be calculated by taking the average of individual results as shown below :

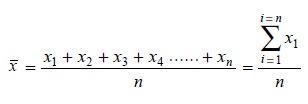
It is evident that the mean of n results is  √n times more reliable than any one of the individual results. Therefore, there exists a diminishing return from accumulating more and more replicate meaurements. In other words, the mean of 9 results is 3 times as reliable as 1 result in measuring central tendency (i.e., the value about which the individual results tend to cluster) ; the mean of 16 results is 4 times as reliable etc.

2. Median

The median of an even number of results is nothing but the average of the ‘two middle values’ pro-vided the results are listed in order ; whereas for an odd number of results the median is the ‘middle value’ itself. However, the ‘mean’ and the ‘median’ are exactly identical in the case of a truly symmetrical distribu-tion. In short, median is an useful measure specifically when dealing with very small samples.

3. Average Deviation (or Mean Deviation)

It is the average of the differences between the individual results and the mean. It is regarded as a measure of variability. In the case of a small number of observations the average deviation is found to be not quite significant statistically. The average or mean distribution may be calculated by adopting the following steps, namely :

(i) To find the differences between individual results and the mean, without considering the +ve or –ve sign,

(ii) To add these individual deviations, and

(iii) To divide by the number of results (i.e., n).

Hence, an ‘average deviation’ may be expressed as :

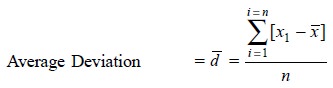
4. Standard Deviation

It is the distance from the mean to the point of inflexion of the normal distribution curve. In compari-son to the average deviation the ‘standard deviation’ is usually considered to be much more useful and meaningful statistically. For a finite number of values it is normally symbolised as ‘S’, and may be expressed as follows :

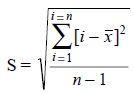
In a situation, where ‘n’ is fairly large, say to the extent of 50 or more, it hardly matters whether the denominator in the above expression is either n – 1 or n; however, the former (i.e., n – 1) is strictly correct.

5. Coefficient of Variation (ν)

The coefficient of variation (ν) is simply the standard deviation(s) expressed as a percentage of the mean ( x’ ) as stated below :

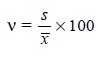
6. Variance (s²)

The variance is the square of the standard deviation(s) i.e., s². However, the former is fundamentally more important in statistics than the latter, whereas the latter is employed more frequently in the treatment of chemical data.

7. Calculations of Fundamental Statistical Parameters

Example : The normality of a solution of sodium hydroxide as determined by an ‘analyst’ by FOUR different titrations are found to be 0.5038 ; 0.5049 ; 0.5042 ; and 0.5039. Calculate the mean, median, average deviation, standard deviation and coefficient of variation.