Significant Figures

SIGNIFICANT FIGURES

Generally, significant figures may be defined as—“All digits* that are certain plus one which contains some uncertainty are said to be significant figures”.

Examples :

(a) Burette Reading : Burettes are mostly graduated with the smallest graduation as 0.1 ml ; hence, while taking the burette reading the figures 6.3 ml can be read off with ample certainty. However, the second place of the decimal is normally estimated by arbitrarily sub-dividing the smallest division into 10 equal parts. Consequently, the final burette reading of 6.32 ml essentially contains three significant figures, of which two are certain, and one with some uncertainty.

(b) Measuring Weights : In the two measured quantities : 4.7350 g and 4.0082 g the zero is a significant figure ; whereas, in the quantity 0.0065 kg the zeros are not significant figures. Thus, in the latter instance the zeros only serve to locate the decimal point and, therefore, may be eliminated completely by proper choice of units, e.g., 6.5 g. Moreover, the first two numbers do have five significant figures, whilst 0.0065 only has two significant figures.

1. Computation Rules

The following computation rules are advocated to make sure that a calculated result, arrived at either by addition and subtraction or multiplication and division essentially contains only the number of ‘digits’ duly justified by the experimental data.

(a) Addition and Subtraction

In addition and subtraction, retain only as many decimal places as appear in the number that has the fewest decimals.

Example : Add algebraically the numbers given : 16.48 + 9.375 – 3.5450 + 118.9.

Following three steps are to be carried out sequentially :

(i) All numbers are required to be rounded up preliminarily to two decimal places,

(ii) Add the rounded numbers, and 

(iii) Final result is then rounded to one decimal place.

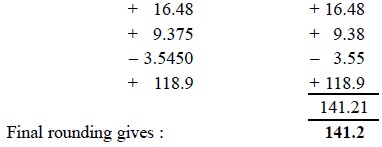
(b) Multiplication and Division

In multiplication or division, retain in each term one more signifcant figure than is contained in the term with the largest uncertainty. However, the percentage precision of product cannot be greater than the percentage precision of the least precise term entering the calculation. Hence, the multi-plication : 2.64 × 3.126 × 0.8524 × 32.9453 must be accomplished using the values

2.64 × 3.126 × 0.852 × 32.95

which is equal to 231.6796. Thus, the result obtained may be expressed to five significant figures as 231.68.

(c) Rounding Numbers

In rounding numbers, always drop the last digit in case it is less than 5, e.g., 8.62 will become 8.6. If the last digit is more than 5, always increase the preceeding digit by one i.e., 9.38 will become 9.4. In case, the digit to be dropped is 5, always round up the preceding digit to the nearest even number i.e., 8.75 will become 8.8 ; and 8.65 will become 8.6. Evidently, this method avoids a tendency to round up numbers in one direction only.

In rounding off quantities to the nearest correct number of significant figures, add one to the last figure retained provided the following figure is either 5 or over. Hence, the average of 0.6526, 0.6521, and 0.6524 is 0.6525 (0.65237).

(d) Always retain as many significant figures in a result as will yield only one uncertain figure.

Examples : (i) A volume read off from a burette reading that lies between 15.6 ml and 15.8 ml must be recorded as 15.7 ml, but not as 15.70 ml, because the latter would indicate that the reading lies between 15.69 and 15.71 ml.

(ii) A weight, to the nearest 0.1 mg, is recorded as 2.4500 g ; and it must not be written as either 2.450 g or 2.45 g, because in the latter instance an accuracy of a centigram is emphasized whereas in the former a milligram.