Comparison of Results

COMPARISON OF RESULTS

In a situation where the same sample has been analysed by two separate techniques altogether, each of them repeated several times, and that the mean values obtained are not the same ; statistically it may be possible to ascertain whether the analytical procedure adopted has been either accurate and precise or if it is superior to one of the two methods.

In fact there are two frequently employed methods that may be used to compare the results, namely :

(a) Student’s t-Test, and

(b) Variance-Ratio Test (or F-Test).

In order to perform these two tests one should have a clear understanding of the statistical term ‘the number of degrees of freedom’.

Degrees of Freedom : It is the number of individual observations which can be allowed to vary under conditions that the mean ( x ) and standard deviation(s), once determined, be held constant.

Thus, a sample having n values have n degrees of freedom, whereas the sum Σ(x – x’ )² is considered to have n – 1 degrees of freedom, because for any defined value of the mean, x’ , only n – 1 value can be assigned freely, as the nth is being defined from the other values automatically.

1. Student’s t-Test

It is usually employed for small samples only. It serves two main objectives, namely :

(i) It is employed to test the difference between the means of two sets of data x₁  and x₂ , and

(ii) It is used to compare the mean obtained from a sample having certain standard value and to express certain degree of confidence in the significance of the comparison.

The value of t may be obtained from the following expression :

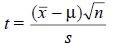                 ........................(i)

where,         x’  = Mean value,

μ = True value,

s = Standard deviation, and

n = Degree of Freedom.

Example : If x the mean of 12 determinations = 9.59, and µ the true value = 9.03, find out whether or not this result is significant provided the standard deviation(s) is 0.16.

From the above Eq. (i) we have :

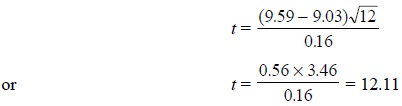
Now, from the t-tables for (n – 1 i.e., 12 – 1 =) 11 degrees of freedom we have :

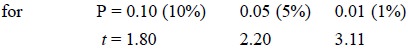
Evidently, the calculated value for t is 12.11 and the result is highly significant. Besides, the t-table also gives the information that the probability of obtaining the difference of 0.56 between the experimental and the true result comes out to be less than 1 in 100, which obviously is indicative of the fact that some kind of bias does exist in the laboratory method adopted.

2. Variance-Ratio Test (or F-Test)

A test that makes use of the ratio of the variances of two sets of results to determine if the standard deviations (s) are significantly different. Its application may also be extended to compare precisely the results obtained either from two different laboratories or from two different analytical procedures.

It is simply calculated from the following equation :

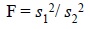                                  ...................(ii)

where, s₁ and s₂ = Standard deviations of two sets of results.

Various steps invoived to determine F-Test are

(i) Find the ratio from Eq. (ii),

(ii) Place the larger s-value in the numerator so that F > 1,

(iii) Check for its significance against values in the F-table, and

(iv) If the F-value in the table is less than the calculated F-value, then the two standard deviations are significantly different ; otherwise, they are not.

Example : A sample of anhydrous sodium carbonate (Na₂CO₃) is analysed by two different methods which give the results for the percentage of Na₂CO₃ as follows :

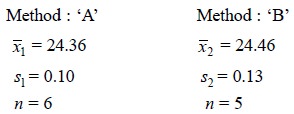
Is there any significant difference between the precision of these two sets of results ?

Applying the variance-ratio or F-Test from Eq. (ii) we have :

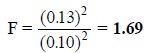
From the standard table having F-values at the 95% probability level, under column n – 1 = 4 (since s₂ >s_l ) and row n – 1 = 5, find F = 6.39. Because, 6.39 > 1.69, the standard deviations are not significantly different [see step (iv) above].