Roundness Measurement

ROUNDNESS MEASUREMENTS

Roundness is defined as a condition of a surface of revolution. Where all points of the surface intersected by any plane perpendicular to a common axis in case of cylinder and cone.

Devices used for measurement of roundness

1) Diametral gauge.

2)  Circumferential conferring gauge => a shaft is confined in a ring gauge and rotated against a set indicator probe.

3) Rotating on center

4) V-Block

5) Three-point probe.

6) Accurate spindle.

1. Diametral method

The measuring plungers are located 180° a part and the diameter is measured at several places. This method is suitable only when the specimen is elliptical or has an even number of lobes. Diametral check does not necessarily disclose effective size or roundness. This method is unreliable in determining roundness.

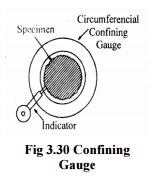
1.     Circumferential confining gauge

Fig. shows the principle of this method. It is useful for inspection of roundness in production. This method requires highly accurate master for each size part to be measured. The clearance between part and gauge is critical to reliability. This technique does not allow for the measurement of other related geometric characteristics, such as concentricity, flatness of shoulders etc.

3. Rotating on centers

The shaft is inspected for roundness while mounted on center. In this case, reliability is dependent on many factors like angle of centers, alignment of centres, roundness and surface condition of the centres and centre holes and run out of piece. Out of straightness of the part will cause a doubling run out effect and appear to be roundness error.

2.     V-Block

The set up employed for assessing the circularity error by using V Block is shown in fig.

The V block is placed on surface plate and the work to be checked is placed upon it. A diameter indicator is fixed in a stand and its feeler made to rest against the surface of the work. The work is rotated to measure the rise on fall of the workpiece. For determining the number of lobes on the work piece, the work piece is first tested in a 60° V-Block and then in a 90° V-Block. The number of lobes is then equal to the number of times the indicator pointer deflects through 360° rotation of the work piece.

Limitations

a) The circularity error is greatly by affected by the following factors.

(i)   If the circularity error is i\e, then it is possible that the indicator shows no variation.

(ii) Position of the instrument i.e. whether measured from top or bottom.

(iii) Number of lobes on the rotating part.

b)  The instrument position should be in the same vertical plane as the point of contact of the part with the V-block.

c) A leaf spring should always be kept below the indicator plunger and the surface of the part.

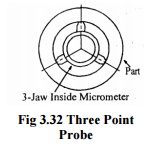
5. Three point probe

The fig. shows three probes with 120° spacing is very, useful for determining effective size they perform like a 60° V-block. 60° V-block will show no error for 5 a 7 lobes magnify the error for 3-lobed parts show partial error for randomly spaced lobes.

Roundness measuring spindle

There are following two types of spindles used.

1.Overhead spindle

Part is fixed in a staging plat form and the overhead spindle carrying the comparator rotates separately from the part. It can determine roundness as well as camming (Circular flatness). Height of the work piece is limited by the location of overhead spindle. The concentricity can be checked by extending the indicator from the spindle and thus the range of this check is limited.

2.Rotating table

Spindle is integral with the table and rotates along with it. The part is placed over the spindle and rotates past a fixed comparator

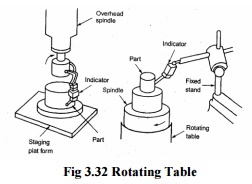
Fig 3.32 Rotating Table

Roundness measuring machine

Roundness is the property of a surface of revolution, where all points on the surface are equidistant from the axis. The roundness of any profile can be specified only when same center is found from which to make the measurements. The diameter and roundness are measured by different method and instruments. For measurement of diameter it is done statically, for measuring roundness, rotation is always necessary. Roundness measuring instruments are two types.

1. Rotating pick up type.

2. Turn table type.

These are accurate, speed and reliable measurements. The rotating pick up type the work piece is stationary and the pickup revolved. In the turn table the work piece is rotated and pick up is stationery. On the rotating type, spindle is designed to carry the light load of the pickup. The weight of the work piece, being stationary and is easy to make. In the turn table type the pickup is not associated with the spindle. This is easier to measure roundness. Reposition the pickup has no effects on the reference axis.

The pickup converts the circuit movement of the stylus into electrical signal, which is processed and amplified and fed to a polar recorder. A microcomputer is incorporated with integral visual display unit and system is controlled from compact keyboards, which increases the system versatility, scope and speed of analysis. System is programmed to access the roundness of work piece with respect to any four of the internationality recognized reference circles. A visual display of work piece profile can be obtained. Work piece can be assessed over a circumference, and with undercut surface or an interrupted surface with sufficient data the reference circle can be fitted to the profile. The program also provides functions like auto centering, auto ranging, auto calibration and concentricity.

Modern Roundness Measuring Instruments

This is based on use of microprocessor to provide measurements of roundness quickly and in a simple way; there is no need of assessing out of roundness. Machine can do centering automatically and calculate roundness and concentricity, straightness and provide visual and digital displays. A computer is used to speed up calculations and provide the stand reference circle.

(i) Least square circle

The sum of the squares of a sufficient no. of equally spaced radial ordinates measured from the circle to the profile has minimum value. The center of such circle is referred to as the least square center. Out of roundness is defined as the radial distance of the maximum peak from the circle (P) plus the distance of the maximum valley from this circle.

(ii) Minimum zone or Minimum radial separation circle

These are two concentric circles. The value of the out of roundness is the radial distance between the two circles. The center of such a circle is termed as the minimum zone center. These circles can be found by using a template.

(iii) Maximum inscribed circle

This is the largest circle. Its center and radius can be found by trial and error by compare or by template or computer. Since V = 0 there is no valleys inside the circle.

(iv)Minimum circumscribed circles

This is the smallest circle. Its center and radius can be found by the previous method since P = 0 there is no peak outside the circle. The radial distance between the minimum circumscribing circle and the maximum inscribing circle is the measure of the error circularity. The fig shows the trace produced by a recording instrument.

This trace to draw concentric circles on the polar graph which pass through the maximum and minimum points in such way that the radial distance be minimum circumscribing circle containing the trace or the n inscribing circle which can fitted into the trace is minimum. The radial distance between the outer and inner circle is minimum is considered for determining the circularity error. Assessment of roundness can be done by templates. The out off roundness is defined as the radial distance of the maximum peak (P) from the least square circle plus the distance of the maximum valley (V) from the least square circle. All roundness analysis can be performed by harmonic and slope analysis.