Flatness Testing

FLATNESS TESTING

Flatness testing is possible by comparing the surface with an accurate surface. This method is suitable for small plates and not for large surfaces. Mathematically flatness error of a surface states that the departure from flatness is the minimum separation of a pair of parallel planes which will contain all points on the Surface. The figure which shows that a surface can be considered to be composed of an infinitely large number of lines. The surface will be flat only if all the lines are straight and they lie in the same plane. In the case of rectangular table arc the lines are straight and parallel to the sides of the rectangle in both the perpendicular direction. Even it is not plat, but concave and convex along two diagonals. For verification, it is essential to measure the straightness of diagonals in addition to the lines parallel to the sides.

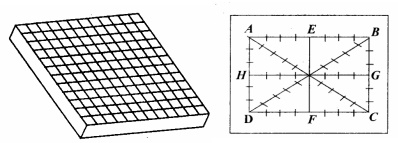
Thus the whole of the surface is divided by straight line. The fig, shows the surface is divided by straight line. The end line AB and AD etc are drawn away from the edges as the edges of the surface are not flat but get worn out by use and can fall off little in accuracy. The straightness of all these lines is determined and then those lines are related with each other in order to verify  whether they lie in the same plane or not.

Procedure for determining flatness

The fig. shows the flatness testing procedure.

(i)               Carry out the straightness test and tabulate the reading up to the cumulative error column.

(ii)             Ends of lines AB, AD and BD are corrected to zero and thus the height of the points A, B and D are zero.

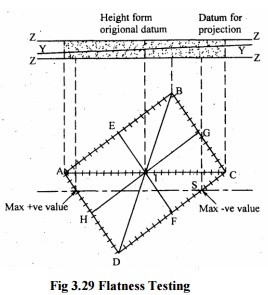
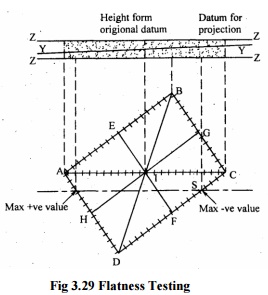
Fig 3.29 Flatness Testing

The height of the point I is determined relative to the arbitrary plane ABD = 000. Point C is now fixed relative to the arbitrary plane and points B and D are set at zero, all intermediate points on BC and DC can be corrected accordingly. The positions of H and G, E and F are known, so it is now possible to fit in lines HG and EF. This also provides a check on previous evaluations since the mid-point of these lines should coincide with the position of mid-point I. In this way, the height of all the points on the surface relative to the arbitrary plane ABD is known.