Properties of Whole Numbers

Properties of Whole Numbers

1. Commutativity of addition and multiplication

When two numbers are added (or multiplied), the order of the numbers does not affect the sum (or the product). This is called commutativity of addition (or multiplication).

Observe the given facts:

43+57 = 57+43

12×15 = 15×12

35,784 + 48,12,69,841 = 48,12,69,841 + 35,784

39,458 × 84,321 = 84,321 × 39,458

Such facts are called as equations. In each of the above equations, the answers on both the sides are same. Finding the answer for the third and fourth equations takes more time. But, these equations are meant to convey the properties of numbers. The third equation is correct by commutativity of addition and the fourth equation is correct by commutativity of multiplication.

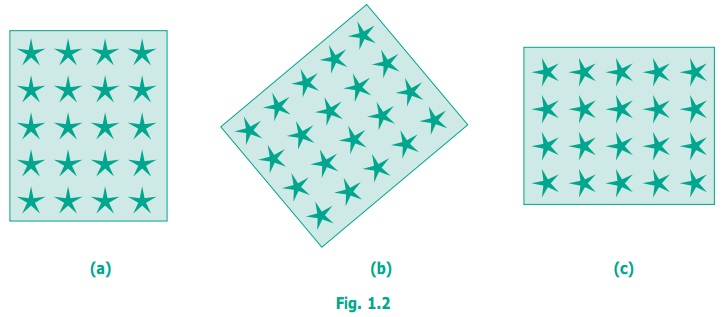
There is a nice pictorial way of understanding commutativity of multiplication. If we have 5 rows of stars, each with 4 stars, we can draw the total of 20 stars as a rectangle (5 × 4 = 20). See Fig.1.2 below. Now rotate the rectangle, Fig.1.2 (a) to get the Fig.1.2(c) as given below. It is the same rectangle. It has exactly the same total number of stars, 20. But now we have 4 rows of stars, each with 5 stars! That is, 5 × 4 = 4 × 5.

Now, look at the following example.

7– 3 = 4 but 3 – 7 will not give the same answer. Similarly, the answers of 12 ÷ 6 and 6 ÷ 12 are not equal.

That is, 7 – 3 ≠ 3 – 7 and 12 ÷ 6 ≠ 6 ÷ 12

Hence, subtraction and division are NOT commutative.

Try these

● Use at least three different pairs of numbers to verify that subtraction is not commutative.

Solution:

Three different pairs

(i) (8 — 3) — 2 ≠  8 — (3 — 2)

5 − 2 ≠  8 − 1

3 ≠ 7

(ii) (6 − 2) − 2 ≠ 6 − (2 − 2)

4 − 2 ≠ 6 − 0

2 ≠ 6

(iii) (10 − 5) − 2 ≠ 10 − ( 5 − 2)

5 − 2 ≠  10 − 3

3 ≠ 7

• Thus we verify that subtraction is not commutative.

● Is 10 ÷ 5, the same as 5 ÷ 10? Justify it by taking two more combinations of numbers.

Solution:

10 ÷ 5  = 2 and 5 ÷ 10 = 1/2

9 ÷ 3 = 3 and 3 ÷ 9 = 1/3

100 ÷ 10 = 10 and 10 ÷ 100 = 1/10

We justify the answer is reciprocal 

2. Associativity of addition and multiplication

When several numbers are added, the order in which the numbers are added does not matter. This is called associativity of addition. Similarly, when several numbers are to be multiplied, the order in which the numbers are multiplied does not matter. This is called associativity of multiplication.

It can be said that the following equations are correct, without actually doing any addition or multiplication, but by using the property of associativity. A few examples are given below:

(43 + 57) + 25                          = 43 + (57 + 25)

12 × (15 × 7)                            = (12 × 15) × 7

35,784 + (48,12,69,841 + 3)    = (35,784 + 48,12,69,841) + 3

(39,458 × 84,321) × 17             = 39,458 × (84,321 × 17)

It is to be noted that here too, subtraction and division are NOT associative.

3. Distributivity of multiplication over addition or subtraction

An interesting fact relating to addition and multiplication comes from the following patterns:

(72 × 13) + (28 × 13)      = (72 + 28) × 13

37 × 102                          = (37 × 100) + (37 × 2)

37×98                              = (37 × 100) – (37 × 2)

In the last two cases, we are actually noting down the following equations:

37 × (100 + 2) = (37 × 100) + (37 × 2)

37 × (100 − 2) = (37 × 100) – (37 × 2)

It can be noted that the product of a number and a sum of numbers can be written as the sum of two products. Similarly, the product of a number and a number got by subtraction can be written as the difference of two products. This property is called as property of distributivity of multiplication over addition or subtraction. It is a very useful property to group numbers in a convenient way. Now let us say 18 × 6 = (10 + 8) × 6 in an easy way as shown in Fig.1.3.

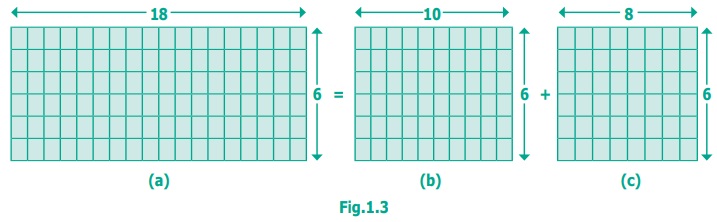
Thus, 18 × 6 = (10 + 8) × 6 is shown clearly in the above figure.

It is to be noted that addition does not distribute over multiplication.

For example,

10 + (10 × 5) = 60 and (10 + 10) × (10 + 5) = 300 are not equal.

4. Identity for addition and multiplication

When zero is added to any number, we get the same number. Similarly, when we multiply any number by 1, we get the same number. So, zero is called the additive identity and one is called the multiplicative identity for whole numbers.

Try these

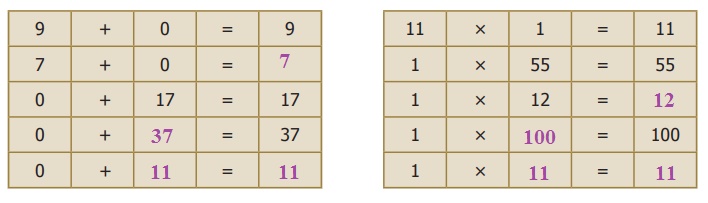
Finally, these are some simple observations that are important.

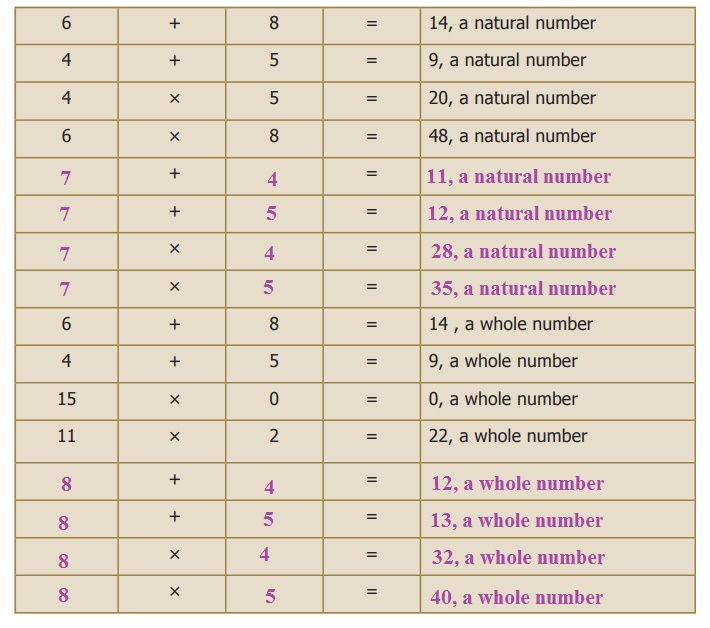
● When we add any two natural numbers, we get a natural number. Similarly when we multiply any two natural numbers, we get a natural number.

● When we add any two whole numbers, we get a whole number. Similarly when we multiply any two whole numbers, we get a whole number.

● When we add a natural number to a whole number, we get a natural number. When we multiply a natural number by a whole number, we get a whole number.

Note

●  Any number multiplied by zero gives zero.

● Division by zero is not defined.

Try these

Complete the table.

All such properties together play a vital role in the Number System. When we learn Algebra, we can realise the usefulness of these properties of the Number System and we can find ways of extending it too.