Estimation of numbers

Estimation of numbers

● Nearly 60,000 people watched the Republic day parade at Rajpath, New Delhi.

● About 2,80,000 people of various countries died due to earthquake and Tsunami on 26th December 2004 in the Indian ocean.

● The India-Pakistan cricket match was viewed by about 30 million cricket fans in the Television all over the world.

We often come across statements like these in TV channels and dailies. Do these news items, give the exact numbers? No. The numbers mentioned are not accurate. They are only the approximate or closer values to the actual ones. This is the reason, why we generally use words like “about”, “nearly” and “approximately”. These numbers are only the estimation of the actual value. The word ‘about’ denotes the number not exactly, but a little more or less. This value is called the estimated value.

The actual figure, though not exactly possible, could have been 59,853 or 61,142 for the first example, and it could have been 2,78,955 or 2,80,984 for the second example. Imagine and write about, what could have been the exact number for the third example given above? Similarly, there are many more possible numbers. Thus,

● to get a rough idea we need estimation.

● to get the estimated value, we generally round off the numbers to their nearest tens, hundreds or thousands.

Some real life situations where we use estimates are

(a) Cost of a Television, Refrigerator, Mixer Grinder etc., is usually expressed in thousands of rupees.

(b) The Voters population in an Assembly Constituency in a state is often stated in lakhs.

(c) The Central or State Government’s Annual Budget is usually given in lakh crore.

When an exact answer is not necessary, estimation strategies can be used to determine a reasonably close answer.

Activity

1. Fill up the jar with some items like Tamarind seeds. Let each student give an estimate of the number of items. Make a table of the result by finding the difference of the estimate and the actual amount.

2. Get a large jar and a bag of Tamarind seeds and put 30 seeds in the jar. Observing the contents, estimate how many seeds roughly will fill the whole jar. Continue to fill the jar to check your estimate.

Rounding off is one way to find a number for estimation that is quite convenient. It gives us the closest suitable number according to a given place value. There are four steps involved in the rounding process. Let us illustrate this with an example.

Example 1.11

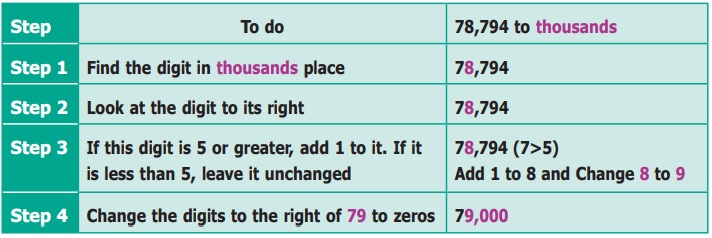
Round off the number 8,436 to the nearest hundreds.

Example 1.12

Round off the number 78,794 to the nearest thousands.

Try these

● Round off the following numbers to the nearest ten.

(i) 57 (ii) 189 (iii) 3,956 (iv) 57,312

Solution:

(i) 57 = 7 > 5 → 60

(ii) 189 = 9 > 5 → 190

(iii) 3,956 = 6 > 5 → 3,960

(iv) 57,312 = 2 < 5 → 57,310

● Round off the following numbers to the nearest ten, hundred and thousand.

(i) 9,34,678 (ii) 73,43,489 (iii) 17,98,45,673

Solution:

Nearest ten

(i) 9,34,678 = 8 > 5 −> 9,34,680

(ii) 73,43,489 = 9 > 5 −> 73,43,490

(iii) 17,98,45,673 = 3 < 5 −> 17,98,45,670

Nearest hundred

(i) 9,34,678 = 7 > 5 −> 9,34,700

(ii) 73,43,489 = 8 > 5 −> 73,43,500

(iii) 17,98,45,673 = 7 > 5 −> 17,98,45,700

Nearest thousand

(i) 9,34,678 = 6 > 5 −> 9,35,000

(ii) 73,43,489  = 4 < 5 −> 73,43,000

(iii)  17,98,45,673 = 6 > 5 −> 17,98,46,000

● The tallest mountain in the world Mount Everest, located in Nepal is 8,848 m high.

Its height can be rounded to the nearest thousand as __________.

Answer: 9000 

1. Estimation of Sum and Difference

Example 1.13

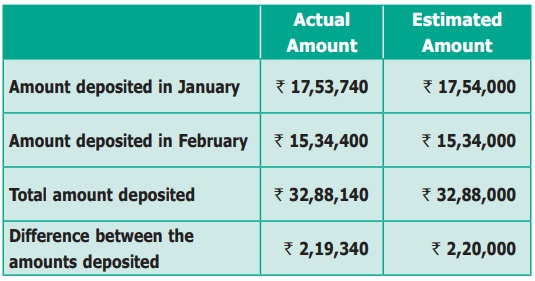
The amount deposited by a Gold merchant in his bank account in the month of January is ₹17,53,740  and in the month of February is ₹15,34,300. Estimate the sum and difference of the amount deposited to the nearest thousand.

Solution

Rounding off to the nearest thousand is as follows.

Think

Is 2,19,340 is rounded off to its nearest thousand as 2,20,000. Why?

 No. Round off value : 2,19,000

2. Estimation of Product and Quotient

Example 1.14

If the cost of a copy of a Thirukkural book is ₹ 188, then find the estimated cost of 31 copies of such books. (Note: Find the rounded values of 188 and 31 and then find the result)

Solution

Here, 188 is nearer to 200 and 31 is nearer to 30.

The exact cost of 31 copies is 188 × 31 = ₹ 5828 whereas,

The estimated cost of 31 copies = 200 × 30 = ₹ 6000

Therefore, the estimated cost of 31 copies of Thirukkural books is ₹ 6000.

Example 1.15

Find the estimated value of 5598 ÷ 689.

Solution

5600 is nearest to 5598

700 is nearest to 689

Hence, the estimated value of 5598 ÷ 689 is 8

Try these

● Estimate the sum and the difference : 8457 and 4573.

Solution:

Actual sum = 8457

                   = 4573

                   13030

8457 + 4573 = 13030

Estimate sum             = 8000

(Nearest to thousand) = 5000

                                     13000

Hence the estimated sum of 8457 + 4573 = 13,000

Actual difference : 8457 − 4573 = ?

                               8457

                               4573

                             3884

8457 − 4573 = 3884

Estimated difference = 8000 − 5000

(Nearest to thousand) = 3000

Hence the estimated difference between 8457 and 4573 is 3000.

● Estimate the product: 39 × 53

Solution:

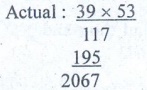
39 × 53 = 2067

Estimated product = 40 × 50

(Nearest to ten) = 2000

Hence the estimated value of 39 × 53 = 2000

● Estimate the quotient: 5546 ÷ 524

Solution:

Hence Estimated quotient of 5546 ÷ 524 = 11