Points to Remember

Maths: Real Numbers

Points to Remember

• When the decimal expansion of p/q , q≠0 terminates that is, comes to an end, the decimal is called a terminating decimal.

• In the decimal expansion of p/q , q≠0 when the remainder is not zero, we have a repeating (recurring) block of digits in the quotient. In this case, the decimal expansion is called non-terminating and recurring.

• If a rational number p/q , q≠0 can be expressed in the form 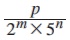, where p ∈ Z and m, n ∈ W, then the rational number will have a terminating decimals. Otherwise, the rational number will have a non-terminating repeating (recurring) decimal.

• A rational number can be expressed either a terminating or a non- terminating recurring decimal.

• An irrational number is a non-terminating and non-recurring decimal, i.e. it cannot be written in form p/q , where p and q are both integers and q ≠ 0.

• The union of all rational numbers and all irrational numbers is called the set of real numbers.

• Every real number is either a rational number or an irratonal number.

• If a real number is not rational number, then it must be an irrational number.

• If ‘a’ is a positive rational number, ‘n’ is a positive integer and if ⁿ√a is an irrational number, then ⁿ√a is called as a surd.

• If ‘m’, ‘n’ are positive integers and a, b are positive rational numbers, then

(i) ( ⁿ√a)ⁿ = a = n√aⁿ (ii) ⁿ√a × ⁿ√b = ⁿ√ab (iii) ^m√ⁿ√a = ^mn√a = ⁿ√^m√a (iv) ⁿ√a / ⁿ√a = ⁿ√[a/b]

• The process of multiplying a surd by another surd to get a rational number is called Rationalisation.

• Expressing a number N in the form of N = a ×10ⁿ where, 1 ≤ a < 10 and ‘n’ is an integer is called as Scientific Notation.