Real Numbers | Maths - Radical Notation | 9th Maths : UNIT 2 : Real Numbers
Chapter: 9th Maths : UNIT 2 : Real Numbers
Radical Notation
Radical Notation
Let
n be a positive integer and r be a real number. If rn
= x, then r is called the nth root of
x and we write
n√x = r
The
symbol n√ (read as nth root) is called a radical; n is the index of the radical (hitherto we named it as
exponent); and x is called the radicand.
Note
It is worth spending some time on the concepts of the ‘square
root’ and the ‘cube root’, for better understanding
of surds.
What happens when n = 2? Then we get r2 = x, so that r is 2√x, our good old friend, the square root of x. Thus 2√16 is written as √16 , and when n =3, we get the cube root of x, namely 3√x . For example, 3√8 is cube root of 8, giving 2. (Is not 8 = 23?)
How
many square roots are there for 4? Since (+2) × (+2) = 4 and also (–2)×(–2) = 4,
we can say that both +2 and –2 are square roots of 4. But it is incorrect to write
that √4 = ± 2 .
This
is because, when n is even, it is an accepted
convention to reserve the symbol n√x for the positive nth
root and to denote the negative nth
root by – n√x. Therefore we
need to write √4 = 2 and −√4 = −2.
When n is odd, for any value of x, there is exactly one real nth root. For example, 3√8
= 2 and 5√−32 = −2.
Thinking Corner
Which one of the following
is false?
(1) The square root of 9 is 3 or –3.
(2) √9 = 3
(3) −√9 = −3
(4) √9 = ±3
1. Fractional Index
Consider
again results of the form r = n√x.
In
the adjacent notation, the index of the radical (namely n which is 3
here) tells you how many times the answer (that is 4) must be multiplied
with itself to yield the radicand.

To
express the powers and roots, there is one more way of representation. It involves
the use of fractional indices.
We
write n√x as x1/n.
With
this notation, for example
3√64
is 641/3 and √25 is 251/2.
Observe
in the following table just some representative patterns arising out of this new
acquaintance:

Example 2.16
Express the following in the form 2n :
(i) 8 (ii) 32 (iii) 1/4 (iv) √2 (v) √8.
Solution
(i) 8 = 2 ×2 × 2 ; therefore 8 = 23
(ii) 32 = 2×2×2×2×2 = 25
(iii) 1/4 = 1/(2×2) = 1/22 = 2−2
(iv) √2 = 21/2
(v) √8 = √2×√2×√2 = (21/2)3 which
may be written as 23/2
Meaning of xm/ n, (where m and n are Positive
Integers)
We interpret xm/n either as the nth
root of the mth power of x or as the mth
power of the nth root of x.
In symbols, xm/n = (xm)1/n or (x1/n)m
= n√xm or (n√x)m
Example 2.17
Find
the value of (i) 815/4 (ii) 64-2/3
Solution
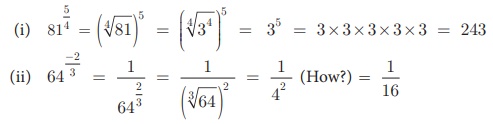
Related Topics