Conjugate Surds | Example Solved Problems | Real Numbers | Maths - Rationalisation of Surds | 9th Maths : UNIT 2 : Real Numbers
Chapter: 9th Maths : UNIT 2 : Real Numbers
Rationalisation of Surds
Rationalisation of Surds
Rationalising
factor is a term with which a term is multiplied or divided to make the whole term
rational.
Examples:
(i) √3 is a rationalising factor of √3 (since √3 × √3
= the rational number 3)
(ii) 7√54 is a rationalising factor
of 7√53 (since their product = 7√57
= 5 , a rational)
Thinking Corner
1. In the example (i) above, can √12 also be a rationalising factor? Can you think of any other number
as a rationalising factor for √3
?
2. Can you think of any other number as a rationalising factor for
7√53 in example
(ii) ?
3. If there can be many rationalising factors for an expression containing
a surd, is there any advantage in choosing the smallest among them for manipulation?
Progress Check
Identify a rationalising factor for each one of the following surds
and verify the same in each case:
(i) √18 (ii) 5√12 (iii) 3√49 (iv) 1/√8
1. Conjugate Surds
Can you guess a rationalising factor for 3 + √2 ? This
surd has one rational part and one radical part. In such cases, the rationalising
factor has an interesting form.
A rationalising factor for 3 + √2 is 3 − √2 . You can
very easily check this.
(3+ √2)(3− √2) = 32− (√2)2
= 9 −2
= 7, a rational.
What could be the rationalising factor for a + √b
where a and b are rational numbers? Is it a − √b ? Check it. What
could be the rationalising factor for √a + √b where a and
b are rational numbers? Is it √a − √b ? Or, is it − √a
+ √b ? Investigate.
Surds
like a + √b and
a − √b are called
conjugate surds. What is the conjugate of √b +a
? It is −
√b +a
. You would have perhaps noted by now
that a conjugate is usually obtained by changing the sign in front of the surd!
Example 2.27
Rationalise
the denominator of
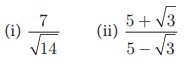
Solution
(i)
Multiply both numerator and denominator by the rationalising factor √14
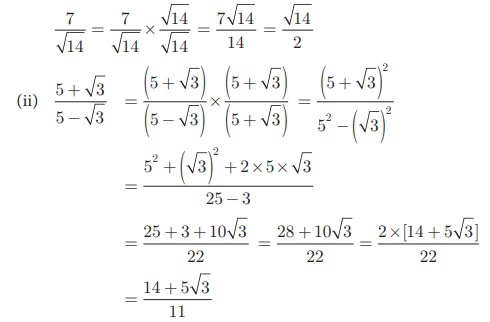
Related Topics