Surds

Surds

Having familiarized with the concept of Real numbers, representing them on the number line and manipulating them, we now learn about surds, a distinctive way of representing certain approximate values.

Can you simplify √4 and remove √ the symbol? Yes; one can replace √4 by the  number 2. How about √[1/9] ? It is easy; without √ symbol, the answer is 1/3. What about √0. 01 ?. This is also easy and the solution is0.1

In the cases of √4 , √[1/9] and √0. 01 , you can resolve to get a solution and make sure that the symbol √ is not seen in your solution. Is this possible at all times?

Consider √18. Can you evaluate it and also remove the radical symbol? Surds are unresolved radicals, such as square root of 2, cube root of 5, etc.

They are irrational roots of equations with rational coefficients.

A surd is an irrational root of a rational number. ⁿ√a is a surd, provided n ∈ ℕ, n > 1, ‘a’ is rational.

Examples : √2 is a surd. It is an irrational root of the equation x² = 2. (Note that x² – 2 = 0 is an equation with rational coefficients. √2 is irrational and may be shown as 1.4142135… a non-recurring, non-terminating decimal).

³√3 (which is same as 3^1/3) is a surd since it is an irrational root of the equation x³ – 3 = 0. (√3 is irrational and may be shown as 1.7320508… a non-recurring, non-terminating decimal).

You will learn solving (quadratic) equations like x² – 6x + 7 = 0 in your next class. This is an equation with rational coefficients and one of its roots is 3 + √2 , which is a surd.

Is √[1/25] a surd? No; it can be simplified and written as rational number 1/5. How about ⁴√[16/81] ? It is not a surd because it can be simplified as 2/3.

The famous irrational number π is not a surd! Though it is irrational, it cannot be expressed as a rational number under the √ symbol. (In other words, it is not a root of any  equation with rational co-efficients).

Why surds are important? For calculation purposes we assume approximate value as √2 = 1.414 , √3 = 1.732 and so on.

 (√2)² = (1.414)² = 1.99936 ≠ 2 ; (√3)² = (1.732)² = 3.999824 ≠ 3

Hence, we observe that √2 and √3 represent the more accurate and precise values than their assumed values. Engineers and scientists need more accurate values while constructing the bridges and for architectural works. Thus it becomes essential to learn surds.

Progress Check

1. Which is the odd one out? Justify your answer.

(i) √36,  √(50/98), √1, √1.44, ⁵√32, √120

(ii) √7, √48, ³√36, √5 + √3, √1.21, √(1/10)

2. Are all surds irrational numbers? − Discuss with your answer.

3. Are all irrational numbers surds? Verify with some examples.

1. Order of a Surd

The order of a surd is the index of the root to be extracted. The order of the surd ⁿ√a is n. What is the order of ⁵√99 ? It is 5.

Surds can be classified in different ways:

(i) Surds of same order : Surds of same order are surds for which the index of the root to be extracted is same. (They are also called equiradical surds).

For example, √x , a^3/2 , ²√m are all 2^nd order (called quadratic) surds .

³√5 , ³√(x -2), (ab)^1/3 are all 3^rd order (called cubic) surds.

√3 , ³√10, ⁴√6 and 8^2/5 are surds of different order.

(ii) Simplest form of a surd : A surd is said to be in simplest form, when it is expressed as the product of a rational factor and an irrational factor. In this form the surd has

(a) the smallest possible index of the radical sign.

(b) no fraction under the radical sign.

(c) no factor is of the form aⁿ, where a is a positive integer under index n.

Example 2.18

Can you reduce the following numbers to surds of same order :

(i) √3 (ii) ⁴√3 (iii) ³√3

Solution

(i) √3= 3^1/2

= 3^6/12

= ¹²√3⁶

= ¹²√729

(ii) ⁴√3 = 3^1/4

= 3^3/12

= ¹²√3³

= ¹²√27

(iii) ³√3 = 3^1/3

= 3^4/12

= ¹²√3⁴

= ¹²√81

The last row has surds of same order.

Example 2.19

1. Express the surds in the simplest form: i) √8 ii) ³√192

2. Show that ³√7 > ⁴√5 .

Solution

1. (i) √8 = √[4×2] = 2√2

(ii) ³√192 = ³√[4×4×4×3] = 4³√3

2. ³√7 =¹²√7⁴ = ¹²√2401

⁴√5 = 5^1/4 = 5^3/12 = ¹²√5³ =¹²√125

¹²√2401 > ¹²√125

Therefore, ³√7 > ⁴√5 .

(iii) Pure and Mixed Surds : A surd is called a pure surd if its coefficient in its simplest form is 1. For example, √3 , ³√6 , ⁴√7 , ⁵√49 are pure surds. A surd is called a mixed surd if its co-efficient in its simplest form is other than 1. For example, 5√3 , 2 ⁴√5 , 3 ⁴√6 are mixed surds.

(iv) Simple and Compound Surds : A surd with a single term is said to be a simple surd. For example, √3 , 2√5 are simple surds. The algebraic sum of two (or more) surds is called a compound surd. For example, √5 + 3√2, √3 −2√7, √5 − 7√2 + 6√3 are compound surds.

(v) Binomial Surd : A binomial surd is an algebraic sum (or difference) of 2 terms both of which could be surds or one could be a rational number and another a surd. For example, 1/2 − √19, 5 + 3√2 , √3 − 2√7 are binomial surds.

Example 2.20

Arrange in ascending order: ³√2 , ²√4, ⁴√3

Solution

The order of the surds ³√2 , ²√4 and ⁴√3 are 3, 2,4.

L.C.M. of 3, 2, 4 = 12.

The ascending order of the surds ³√2, ⁴√3, ²√4 is ¹²√16 < ¹²√27 < ¹²√4096 that is, ³√2, ⁴√3, ²√4.

2. Laws of Radicals

For positive integers m, n and positive rational numbers a and b, it is worth remembering the following properties of radicals:

We shall now discuss certain problems which require the laws of radicals for simplifying.

Example 2.21

Express each of the following surds in its simplest form (i) ³√108 (ii) ³√ (1024)⁻² and find its order, radicand and coefficient.

Solution

 order= 3 ; radicand = 1/4 ; coefficient = 1/64

(These results can also be obtained using index notation).

Note

Consider the numbers 5 and 6. As 5 = √25 and 6 = √36

Therefore, √26, √27, √28, √29, √30, √31, √32, √33, √34, and √35 are surds  between 5 and 6.

Consider 3√2 = √[3²×2] = √18, 2√3= √[2²×3]= √12

Therefore, √17, √15, √14, √13 are surds between 2√3 and 3√2.

3. Four Basic Operations on Surds

(i) Addition and subtraction of surds 

: Like surds can be added and subtracted using the following rules:

aⁿ√b ± cⁿ√b = (a ± c )ⁿ√b , where b > 0.

Example 2.22

 (i) Add 3√7 and 5√7 . Check whether the sum is rational or irrational. (ii) Subtract 4√5 from 7√5 . Is the answer rational or irrational?

Solution

 (i) 3√7+5√7 =(3+5) √7 = 8√7 . The answer is irrational.

 (ii) 7√5 − 4√5 =(7−4) √5 = 3√5 . The answer is irrational.

 Example 2.23

Simplify the following:

(i) √63− √175+ √28 (ii) 2³√40 + 3 ³√625 − 4 ³√320

Solution

 (i) √63− √175+ √28 = √[9×7] – √ [25 ×7] + √ [4×7]

 = 3√7−5√7+2√7

= (3√7 +2√7) − 5√7

= 5√7−5√7

= 0

(ii) 2³√40+3³√625−4³√320

= 2³√[8×5] + 3³√[125×5] −4³√[64×5]

= 2³√[2³×5] +3³√[5³×5]−4³√[4³×5]

= 2×2³√5 + 3×5³√5−4×4³√5

= 4³√5+15³√5−16³√5

= (4+15−16)³√5 = 3³√5

(ii) Multiplication and division of surds

Like surds can be multiplied or divided by using the following rules:

Example 2.24

Multiply ³√40 and ³√16 .

Solution

 ³√40 × ³√16 = (³√[2×2×2×5] ) × (³√[2×2×2×2])

 = (2× ³√5)×(2× ³√2) = 4×(³√2 ׳√5)

 = 4×3√[2×5]

= 4³√10

Example 2.25

Compute and give the answer in the simplest form: 2√72 × 5√32×3√50

Solution

2√72×5√32 × 3√50 = (2×6√2)× (5×4√2)× (3×5√2)

= 2×5×3×6×4×5× √2× √2× √2

= 3600×2√2

= 7200√2

Let us simplify:

√72 = √[36×2] =6√2

√32 = √[16×2]=4√2

√50 = √[25×2] =5√2

Example 2.26

Divide ⁹√8 by ⁶√6 .

Solution

Activity – 1

Is it interesting to see this pattern ?

Verify it. Can you frame 4 such new surds?

Solution:

Activity – 2

Take a graph sheet and mark O, A, B, C as follows.

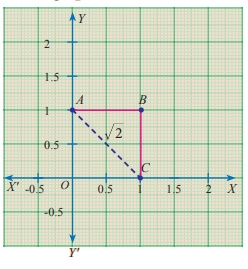
In the square OABC,

OA = AB = BC = OC = 1unit

Consider right angled DOAC

AC = √[1² +1²]

= √2 unit [By Pythagoras theorem]

 The length of the diagonal (hypotenuse)

 AC = √2 , which is a surd.

Consider the following graphs:

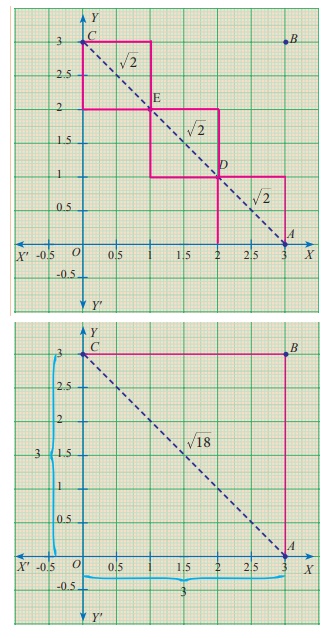
Let us try to find the length of AC in two different ways :

AC = AD +DE +EC

 (diagonals of units squares)

= √2+√2+√2

 AC = 3√2 units

AC = √[OA² +OC²] = √[3² +3²]

= √[9 + 9 ]

AC = √18 units

Are they equal? Discuss. Can you verify the same by taking different squares of different lengths?

Solution: