Decimal Representation to Identify Irrational Numbers

Decimal Representation to Identify Irrational Numbers

It can be shown that irrational numbers, when expressed as decimal numbers, do not terminate, nor do they repeat. For example, the decimal representation of the number π starts with 3.14159265358979, but no finite number of digits can represent π exactly, nor does it repeat.

Consider the following decimal expansions:

(i) 0.1011001110001111…

(ii) 3.012012120121212…

(iii) 12.230223300222333000…

(iv) √2 = 1.4142135624…

Are the above numbers terminating (or) recurring and non- terminating? No… They are neither terminating, nor non–terminating and recurring. Hence they are not rational numbers. They cannot be written in the form of p/q, where p,q, ∈ Z and q≠0. They are irrational numbers.

A number having non- terminating and non- recurring decimal expansion is an irrational number.

Example2.8

Find the decimal expansion of √3

Solution

Thus, by division method, √3 = 1.7320508…

It is found that the square root of every positive non perfect square number is an irrational number. √2, √3, √5, √6, √7 , … are all irrational numbers.

Example 2.9

Classify the numbers as rational or irrational:

Example 2.10

Locate an irrational number between two rational numbers 23/10 and 12/5.

You need an irrational number greater than 2.3 but less than 2.4

One such irrational number is

2.301001000100001000001000000100000001……..

How do you write it?

See the given box for details.

Is this newly found number irrational?

Yes, observe that it is non-terminating and non-recurring.

Can you find an irrational number between 63 and 64 now?

Could it be 63.01001000100001000010000001… … … ?

Between the rational numbers 7.568903 and 7.568904, is it possible that there is this irrational number 7.568903 01 001 0001 00001 000001 0000001… … …?

Example 2.11

Find any 4 irrational numbers between 1/4 and 1/3.

Example 2.12

Find any 3 irrational numbers between 0.12 and 0.13 .

Solution

Three irrational numbers between 0.12 and 0.13 are 0.12010010001…, 0.12040040004…, 0.12070070007…

Example 2.13

Give any two rational numbers lying between 0.5151151115…. and 0.5353353335…

Solution

Two rational numbers between the given two irrational numbers are 0.5152 and 0.5352

For example, when you consider the rational number 4 and the irrational number √5 , then 4 + √5 , 4 – √5 , 4√5 , 4/√5, √5/4........  ------- are all irrational numbers.

Example 2.14

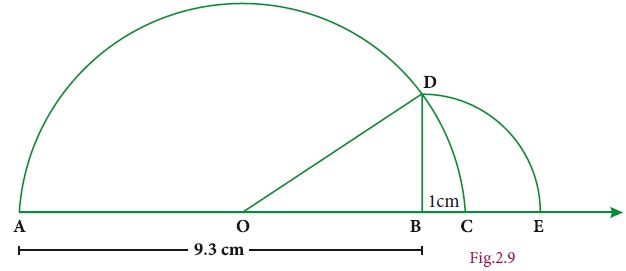
Represent √9.3 on a number line.

Solution

·           Draw a line and mark a point A on it.

·           Mark a point B such that AB = 9.3 cm.

·           Mark a point C on this line such that BC = 1 unit.

·           Find the midpoint of AC by drawing perpendicular bisector of AC and let it be O

·           With O as center and OC = OA as radius, draw a semicircle.

·           Draw a line BD, which is perpendicular to AB at B.

·           Now BD = √9.3 , which can be marked in the number line as the value of BE = BD = √9.3.

The Square Root of a Real Number

You have already come across the concept of the square root of a whole number,  decimal fractions etc. While you easily compute values like √169 (which give whole number answers), you also encounter values like √5, √18 , ... etc that yield irrational solutions.

The number 25 has two square roots 5 and –5. However, when we write √25 , we always mean the positive square root 5 (and not the negative square root –5). The symbol √  denotes the positive square root only.

If a is a rational number, any irrational number of the form √a will sometimes be  referred to as a surd. A real number such as 2√3 will be loosely referred to as surd, since it  can be expressed as √12 (How?). We may also say an expression such as √3 + √2  is a surd, although technically we should say that it is a sum of two surd.

Is the number π a surd? No. It cannot be expressed as the root of a rational number, or a finite combination of such numbers.

Recall the basic rules for square roots:

If a,b are positive numbers, then

Example2.15

Find whether x and y are rational or irrational in the following.