Exercise 2.9: One Mark Multiple Choose the correct Answers

Real Numbers

Exercise 2.9

1. If n is a natural number then √n is

(1) always a natural number.

(2) always an irrational number.

(3) always a rational number

(4) may be rational or irrational

[ Answer: (4) may be rational or irrational ]

2. Which of the following is not true?.

(1) Every rational number is a real number.

(2) Every integer is a rational number.

(3) Every real number is an irrational number.

(4) Every natural number is a whole number.

Solution: Real numbers contain rationals and irrationals.

[ Answer: (3) Every real number is an irrational number]

3. Which one of the following, regarding sum of two irrational numbers, is true?

(1) always an irrational number.

(2) may be a rational or irrational number.

(3) always a rational number.

(4) always an integer.

[ Answer: (2) may be a rational or irrational number]

4. Which one of the following has a terminating decimal expansion?.

(1) 5/64

(2) 8/9

(3) 14/15

(4) 1/12

Solution: 5/64 = 5/2⁶

[ Answer: (1) 5/64 ]

5. Which one of the following is an irrational number

(1) √25

(2) √(9 /4)

(3) 7/11

(4) π

Solution: π represents a irrational number

[ Answer: (4) π]

6. An irrational number between 2 and 2.5 is

(1) √11

(2) √5

(3) √2.5

(4) √8

Solution: 2² = 4 and 2.5² = 6.25

[ Answer: (2) √5]

7. The smallest rational number by which 1/3 should be multiplied so that its decimal expansion terminates with one place of decimal is

(1) 1/10

(2) 3/10

(3) 3

(4) 30

Solution: 3/10 is the small number.

[ Answer: (2) 3/10]

8. If 1/7 = 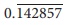 then the value of 5/7 is

Solution:

[ Answer: (2) ]

9. Find the odd one out of the following.

(1) √32 × √2

(2) √27 / √3

(3) √72 × √8

(4) √54 / √18

Solution:  

√72 × √8 = √[9×8] × √8 = 3×8 = 24;

√32 × √2 = √[16×2] × √2 = 4×2=8;

√27 ÷ √3 = √[9×3] × √3 = 3×3=9;

√54 ÷ √18 = √[3×18] × √18 = √3×18=18√3;

[Answer: (4) √54 ÷ √18 ]

10. 

Solution: 0.343434… + 0.344444…

[ Answer: (1) ]

11. Which of the following statement is false?

(1) The square root of 25 is 5 or −5

(2) – √25 = −5

 (3) √25 = 5

 (4) √25 = ± 5

[ Answer: (4) √25 = ± 5]

12. Which one of the following is not a rational number?

(1) √[8/18]

(2) 7/3

(3) √0. 01

(4) √13

Solution:

√(8/18) = √(4/9) = 2/3 is a rational number;

7/3 is a rational number

√0.01 - √(1/100)=1/10 is a rational number

√13 is not a rational number

 [ Answer: (4) √13]

13. √27+ √12 =

(1) √39

(2) 5√6

(3) 5√3

(4) 3√5

Solution: √27 + √12 = √[9×3] + √[4×3] = 3√3 + 2√3 = 5√3

[ Answer: (3) 5√3]

14. If √80 = k√5, then k =

(1) 2

(2) 4

(3) 8

(4) 16

Solution: √80 = √[16×5] = 4√5 = k√5 ⇒ k=4

[ Answer: (2) 4]

15. 4√7×2√3=

(1) 6√10

(2) 8√21

(3) 8√10

(4) 6√21

Solution: 4√7 × 2√3 = 8 × √[7×3] = 8√21

[ Answer: (2) 8√21]

16. When written with a rational denominator, the expression 2√3 / 3√2 can be simplified as

(1) √2 / 3

(2) √3 / 2

(3) √6  / 3

(4) 2  / 3

Solution: 2√3 / 3√2 = 2√3 × √2 / 3√2 × √2 = 2√6 / 3×2 = 2√6 / 6 = √6/3

[ Answer: (3) √6  / 3]

17. When (2√5 − √2)² is simplified, we get

 (1) 4√5+2√2

(2) 22-4√10

(3) 8-4√10

(4) 2√10-2

Solution: (2√5 - √2)² = (2√5)² – 2 × 2√5 × √2 +√2²

= 4×5 – 4√10 + 2 = 22 - 4√10

 [ Answer: (2) 22-4√10 ]

18. ( 0. 000729 )^-3/4 × (0.09 )^-3/4 = ______

(1) 10³ / 3³

(2) 10⁵  / 3⁵

(3) 10²  / 3²

(4) 10⁶ / 3⁶

Solution:

[ Answer: (4) 10⁶ / 3⁶ ]

19. If √9^{x = 3}√9² , then x = ______

(1) 2 / 3

(2) 4 / 3

(3) 1 / 3

(4) 5/ 3

Solution: (9^x)^1/2 = (9²)^1/3

⇒ 9^x/2 = 9^2/3

⇒ x/3 = 2/3

3x = 4

x= 4/3

[ Answer: (2) 4 / 3 ]

20. The length and breadth of a rectangular plot are 5×10⁵ and 4×10⁴ metres respectively. Its area is ______.

(1) 9×10¹ m²

(2) 9×10⁹ m²

(3) 2×10¹⁰ m²

(4) 20×10²⁰ m²

Solution:

 l =5 × 10⁵ metres; b = 4 × 10⁴ metres

 Area = l × b = 5 × l0⁵ × 4 × l0⁴ = 20 x 10⁵⁺⁴ = 20 × 10⁹ = 2.0 x 10¹ × 10⁹

= 2 × 10¹⁰ m²

[ Answer: (3) 2×10¹⁰ m² ]