Perceptual Constancy

PERCEPTUAL CONSTANCY

We began earily by noting that perception seems easy and immediate—we open our eyes and see, with no apparent complexities. But we also said that this intu-ition is misleading, because perception involves considerable complexities—many steps to be taken, and many points at which the perceiver must play an active role in interpreting the input. This message emerged again and again in our discussion of how we recognize the objects that surround us, and the same broad message—mul-tiple steps, and an active role—emerges when we consider another essential aspect of perceiving: the achievement of perceptual constancy. This term refers to the fact that we perceive the constant properties of objects in the world (their sizes, shapes, and so on) even though the sensory information we receive about these attributes changes whenever our viewing circumstances change.

To illustrate this point, consider the perception of size. If we happen to be far away from the object we’re viewing, then the image cast onto our retinas by that object will be relatively small. If we approach the object, then the image size will increase. We’re not fooled by this variation in image size, though. Instead, we manage to achieve sizeconstancy—correctly perceiving the sizes of objects in the world despite the changes inretinal-image size created by changes in viewing distance. Likewise, if we view a door straight on, the retinal image will be rectangular in shape; but if we view the same door from an angle, the retinal image will have a different shape (Figure 5.20). Still, we achieve shape constancy—that is, we correctly perceive the shapes of objects despite changes in the retinal image created by shifts in our viewing angle. We also achieve brightness constancy—we correctly perceive the brightness of objects whether they’reilluminated by dim light or strong sun.

Unconscious Inference

How do we achieve each of these forms of constancy? One hypothesis focuses on rela-tionships within the retinal image. In judging size, for example, we might be helped bythe fact that we generally see objects against some background, and various elements in the background can provide a basis for comparison with the target object. Thus the dog sitting nearby on the kitchen floor is half as tall as the chair and hides a number of the kitchen’s floor tiles from view. If we take several steps back from the dog, none of these relationships changes, even though the sizes of all the retinal images are reduced (Figure 5.21). Size constancy, therefore, might be achieved by focusing not on the images themselves but on these unchanging relationships.

Relationships do contribute to size constancy, and that’s why we are better able to judge size when comparison objects are in view or when the target we’re judging sits on a surface that has a uniform visual texture (like the floor tiles in the example). But these relationships don’t tell the whole story. Size constancy is found even when the visual scene offers no basis for comparison—if, for example, the object to be judged is the only object in view—provided that other cues signal the distance of the target object (Chevrier & Delorme, 1983; Harvey & Leibowitz, 1967; Holway & Boring, 1947).

How might our visual system use this distance information? More than a century ago, the German physicist Hermann von Helmholtz developed an influential hypoth-esis regarding this question. Helmholtz started with the fact that there’s a simple inverse relationship between distance and retinal image size: If an object doubles its distance from the viewer, the size of its image is reduced by half. If an object triples its distance, the size of its image is reduced to a third of its initial size. This relation-ship is guaranteed to hold true because of the principles of optics, and the relation-ship makes it possible for perceivers to achieve size constancy by means of a simple calculation. Of course, Helmholtz knew that we don’t run through a conscious calcu-lation every time we perceive an object’s size; but he believed we were calculating nonetheless—and so he referred to the process as an unconscious inference (Helmholtz, 1909).

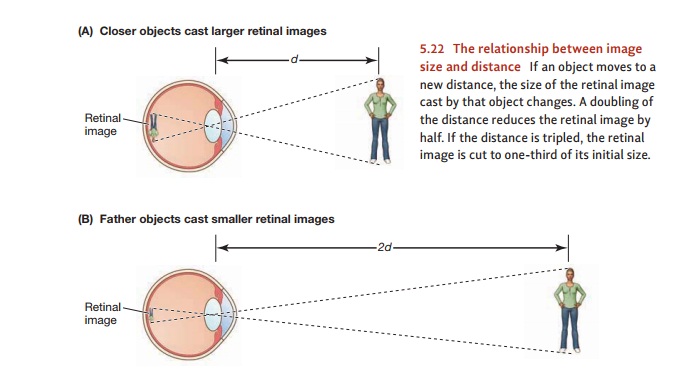
What is the calculation that allows someone to perceive size correctly? It’s simply multiplication: the size of the image on the retina, multiplied by the distance between you and the object. (We’ll have more to say about how you know this distance in a later section.) Thus, imagine an object that, at a distance of 10 feet, casts an image on the

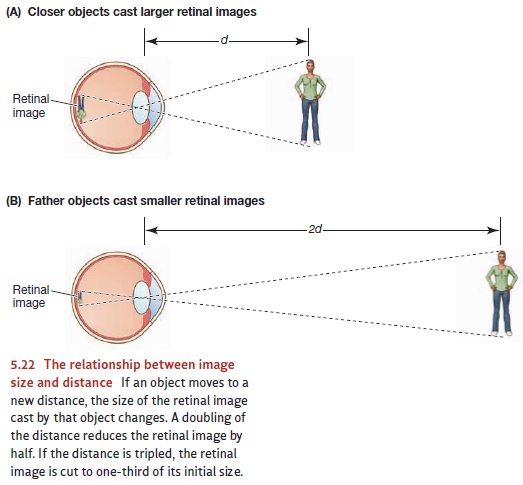
retina that’s 4 millimeters across (Figure 5.22). The same object, at a distance of 20 feet, casts an image of 2 millimeters. In both cases, the product—10 # 4 or 20 # 2—is the same. If, therefore, your size estimate depends on that product, your size estimate won’t be thrown off by viewing distance—and of course, that’s exactly what we want.

What’s the evidence that size constancy does depend on this sort of inference? In many experiments, researchers have shown people some object and, without changing the object’s retinal image, changed the apparent distance of the object. (There are many ways to do this—lenses that change how the eye has to focus to bring the object into sharp view, or mirrors that change how the two eyes have to angle inward so that the object’s image is centered on both foveas.) If people are—as Helmholtz proposed— using distance information to judge size, then these manipulations should affect size perception. Any manipulation that makes an object seem farther away (without chang-ing retinal image size) should make that object seem bigger. Any manipulation that makes the object seem closer should make it look smaller. And, in fact, these predictions are correct—a powerful confirmation that we do use distance to judge size.

A similar proposal explains how people achieve shape constancy. Here, we take the slant of the surface into account and make appropriate adjustments—again, an unconscious inference—in our interpretation of the retinal image’s shape. Likewise for brightness constancy: We seem to be quite sensitive to how a surface is oriented relative to the available light sources, and we take this information into account in estimating how much light is reaching the surface. Then we use this assessment of lighting to judge the surface’s brightness (e.g., whether it’s black or gray or white). In all these cases, therefore, it appears that our perceptual system does draw some sort of unconscious inference, taking our viewing circumstances into account in a way that allows us to perceive the constant properties of the visual world.

Illusions

This process of taking information into account—no matter whether we’re taking viewing distance into account, or viewing angle, or illumination—is crucial for achiev-ing constancy. More than that, it’s yet another indication that we don’t just “receive”

Visual information,weinterpretit.The interpretation is always an essential partof  our perception and generally helps us perceive the world correctly. But the role of th  interpretation becomes especiallyclear  when  we  misinterpret  the  informa-tion  available  to  us  and  end  up  misper-ceiving the world.

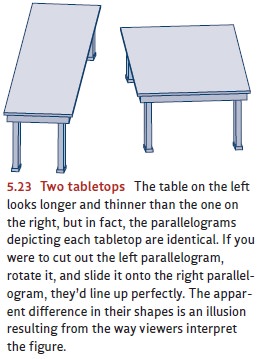
Consider  the  two  tabletops  shown  in Figure 5.23. The table on the left looksappreciably longer and thinner than the one on the right; a tablecloth that fits one table surely won’t fit the other. Objectively, though, the parallelogram depicting the left table-top is exactly the same shape as the one depicting the right tabletop. If you were to cut out the left tabletop, rotate it, and slide it onto the right tabletop, they’d be an exact match.

Why do people misperceive these shapes? The answer involves the normal mecha-nisms of shape constancy. Cues to depth in this figure cause the viewer to perceive the figure as a drawing of two three-dimensional objects, each viewed from a particular angle. This leads the viewer—quite automatically—to adjust for the (apparent) viewing angles in order to perceive the two tabletops, and it’s this adjustment that causes the illusion. Notice then, that this illusion about shape is caused by a misperception of depth: The viewer misperceives the depth relationships in the drawing and then takesthis faulty information into account in interpreting the shapes. (For a related illusion, see Figure 5.24.)

A different example is shown in Figure 5.25. It seems obvious to most viewers that the center square in this checkerboard (third row, third column) is a brighter shade than the square indicated by the arrow. But, in truth, the shade of gray shown is identical for these two squares. What has happened here? The answer again involves the normal mechanisms of perception. Notice, first, that the central square is surrounded by dark squares; this arrangement creates a contrast effect that makes the central square look brighter. The square marked at the edge of the checkerboard, on the other hand, is surrounded by white squares; here, contrast makes the marked square look darker. So for both squares, we have contrast effects that move us toward the illusory perception. But the visual system also detects that the central square is in the shadow cast by the cylinder. Our vision compensates for this fact—again, an example of unconscious inference that takes the shadow into account in judging brightness—and powerfully magnifies the illusion.