Optimizing for Parallelism and Locality

Chapter 11

Optimizing for Parallelism and Locality

This chapter shows how a compiler can enhance parallelism and locality in com-putationally intensive programs involving arrays to speed up target programs running on multiprocessor systems. Many scientific, engineering, and commer-cial applications have an insatiable need for computational cycles. Examples include weather prediction, protein-folding for designing drugs, fluid-dynamics for designing aeropropulsion systems, and quantum chromodynamics for study-ing the strong interactions in high-energy physics.

One way to speed up a computation is to use parallelism. Unfortunately, it is not easy to develop software that can take advantage of parallel machines. Dividing the computation into units that can execute on different processors in parallel is already hard enough; yet that by itself does not guarantee a speedup. We must also minimize interprocessor communication, because communication overhead can easily make the parallel code run even slower than the sequential execution!

Minimizing communication can be thought of as a special case of improving a program's data locality. In general, we say that a program has good data locality if a processor often accesses the same data it has used recently. Surely if a processor on a parallel machine has good locality, it does not peed to com-municate with other processors frequently. Thus, parallelism and data locality need to be considered hand-in-hand. Data locality, by itself, is also important for the performance of individual processors. Modem processors have one or more level of caches in the memory hierarchy; a memory access can take tens of machine cycles whereas a cache hit would only take a few cycles. If a program does not have good data locality and misses in the cache often, its performance will suffer.

Another reason why parallelism and locality are treated together in this same chapter is that they share the same theory. If we know how to optimize for data locality, we know where the parallelism is. You will see in this chapter that the program model we used for data-flow analysis in Chapter 9 is inadequate for parallelization and locality optimization. The reason is that work on data-flow analysis assumes we don't distinguish among the ways a given statement is reached, and in fact these Chapter 9 techniques take advantage of the fact that we don't distinguish among different executions of the same statement, e.g., in a loop. To parallelize a code, we need to reason about the dependences among different dynamic executions of the same statement to determine if they can be executed on different processors simultaneously.

This chapter focuses on techniques for optimizing the class of numerical applications that use arrays as data structures and access them with simple regular patterns. More specifically, we study programs that have affine array accesses with respect to surrounding loop indexes. For example, if i and j are the index variables of surrounding loops, then Z[i][j] and Z[i][i + j] axe affine accesses. A function of one or more variables, ii,i₂,... ,i_n is affine if it can be expressed as a sum of a constant, plus constant multiples of the variables, i.e., Co + c1X1 + c₂x₂ + • • • + c_nx_n, where Co, c i , . . . , c_n are constants. Affine functions are usually known as linear functions, although strictly speaking, linear functions do not have the CQ term.

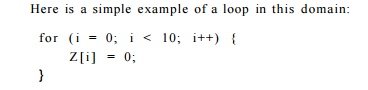
Because iterations of the loop write to different locations, different processors can execute different iterations concurrently. On the other hand, if there is another statement Z [ j ] = 1 being executed, we need to worry about whether i could ever be the same as j, and if so, in which order do we execute those instances of the two statements that share a common value of the array index.

Knowing which iterations can refer to the same memory location is impor-tant. This knowledge lets us specify the data dependences that must be honored when scheduling code for both uniprocessors and multiprocessors. Our objective is to find a schedule that honors all the data dependences such that operations that access the same location and cache lines are performed close together if possible, and on the same processor in the case of multiprocessors.

The theory we present in this chapter is grounded in linear algebra and integer programming techniques. We model iterations in an n-deep loop nest as an n-dimensional polyhedron, whose boundaries are specified by the bounds of the loops in the code. Affine functions map each iteration to the array locations it accesses. We can use integer linear programming to determine if there exist two iterations that can refer to the same location.

The  set  of code transformations we  discuss here fall into two categories:

affine  partitioning  and  blocking. Affine partitioning  splits up the  polyhedra of iterations into components, to be executed either on different machines or one-by-one sequentially.  On the other hand, blocking creates a hierarchy of iterations.  Suppose we are given a loop that sweeps through an  array row-by- row. We may instead subdivide the array into blocks and visit all elements in a block before moving to the next. The resulting code will consist of outer loops traversing the blocks, and then inner loops to sweep the elements within each block. Linear algebra techniques are used to determine both the best affine partitions and the best blocking schemes.

In the following, we first start with an overview of the concepts in parallel computation and locality optimization in Section 11.1. Then, Section 11.2 is an extended concrete example — matrix multiplication — that shows how loop transformations that reorder the computation inside a loop can improve both locality and the effectiveness of parallelization.

Sections 11.3 to Sections 11.6 present the preliminary information necessary for loop transformations. Section 11.3 shows how we model the individual iterations in a loop nest; Section 11.4 shows how we model array index functions that map each loop iteration to the array locations accessed by the iteration; Section 11.5 shows how to determine which iterations in a loop refer to the same array location or the same cache line using standard linear algebra algorithms; and Section 11.6 shows how to find all the data dependences among array references in a program.

The rest of the chapter applies these preliminaries in coming up with the optimizations. Section 11.7 first looks at the simpler problem of finding par-allelism that requires no synchronization. To find the best affine partitioning, we simply find the solution to the constraint that operations that share a data dependence must be assigned to the same processor.

Well, not too many programs can be parallelized without requiring any synchronization. Thus, in Sections 11.8 through 11.9.9, we consider the general case of finding parallelism that requires synchronization. We introduce the concept of pipelining, show how to find the affine partitioning that maximizes the degree of pipelining allowed by a program. We show how to optimize for locality in Section 11.10.  Finally, we discuss how affine transforms are useful for optimizing for other forms of parallelism.