Chapter: Compilers : Principles, Techniques, & Tools : Optimizing for Parallelism and Locality
Affine Array Indexes
Affine Array Indexes
1 Affine Accesses
2 Affine and Nonaffine Accesses
in Practice
3 Exercises for Section 11.4
The focus of this chapter is on the class of affine array
accesses, where each array index is expressed as affine expressions of loop
indexes and symbolic constants. Affine functions provide a succinct mapping
from the iteration space to the data space, making it easy to determine which
iterations map to the same data or same cache line.
Just as the affine upper and lower bounds of a loop can be
represented as a matrix-vector calculation, we can do the same for affine
access functions. Once placed in the matrix-vector form, we can apply standard
linear algebra to find pertinent information such as the dimensions of the data
accessed, and which iterations refer to the same data.
1. Affine Accesses
We say that an array
access in a loop is affine if
1.
The bounds of
the loop are expressed as affine expressions of the sur-rounding loop variables
and symbolic constants, and
2.
The index for
each dimension of the array is also an affine expression of surrounding loop
variables and symbolic constants.
Example 1 1 . 1 6 : Suppose
i and j are loop index variables bounded by affine expressions. Some examples of affine array accesses are
Z[i], Z[i + j + 1], Z[0], Z[i, i], and Z[2*i +1,3* j — 10]. If n is a symbolic constant for a loop nest,
then Z[S * n, n — j] is another example of an affine array access. However, Z[i
* j] and Z[n * j] are not affine accesses.
Each affine array access can be described by two matrices and two
vectors. The first matrix-vector pair is the B and b that
describe the iteration space for the access, as in the inequality of Equation
(11.1). The second pair, which we usually refer to as F and f,
represent the function(s) of the loop-index variables that produce the array
index(es) used in the various dimensions of the array access.
Formally, we represent an array access in a loop nest that uses a
vector of index variables i by the four-tuple T =
(F,f,B>b); it maps a vector i within the bounds

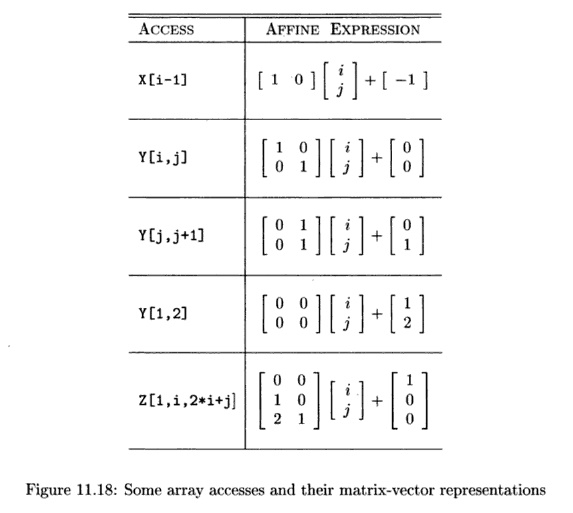
Example 11 . 17: In Fig. 11.18 are some common array accesses,
expressed in matrix notation. The two
loop indexes are i and j, and these form the vector i. Also, X, Y, and Z are
arrays with 1, 2, and 3 dimensions, respectively. The first access, A[i - 1],
is represented by a 1 x 2 matrix F and a vector f of length 1. Notice that when
we perform the matrix-vector multiplication and add in the vector f, we are
left with a single function, which is exactly the formula for the access to the
one-dimensional array X. Also notice the
third access, Y[j,j + 1], which, after matrix-vector multiplication and
addition, yields a pair of functions,
(J,j + 1). These are the indexes
of the two dimensions of the array access.
Finally, let us observe the fourth access K[l,2] . This access is
a constant, and unsurprisingly the matrix F is all 0's. Thus, the vector
of loop indexes, i, does not appear in the access function.
2. Affine
and Nonaffine Accesses in Practice
There
are certain common data access patterns found in numerical programs that fail
to be affine. Programs involving sparse matrices are one important example. One
popular representation for sparse matrices is to store only the nonzero
elements in a vector, and auxiliary index arrays are used to mark where a row
starts and which columns contain nonzeros. Indirect array accesses are used in
accessing such data. An access of this type, such as is a nonaffine access to
the array X. If the sparsity is regular, as in banded matrices having
nonzeros only around the diagonal, then dense arrays can be used to represent
the subregions with nonzero elements. In that case, accesses may be affine.
Another
common example of nonaffine accesses is linearized arrays. Pro-grammers
sometimes use a linear array to store a logically multidimensional object. One
reason why this is the case is that the dimensions of the array may not be
known at compile time. An access that would normally look like Z[i,j] would
be expressed as Z[i * n + j], which is a quadratic function. We can
convert the linear access into a multidimensional access if every access can be decomposed into separate dimensions with the guarantee
that none of the components exceeds its bound. Finally, we note that
induction-variable analy-ses can be used to convert some nonaffine accesses
into affine ones, as shown in Example 11.18.

to make the access to matrix Z affine.
3. Exercises for Section 11.4
Exercise 11.4.1 : For each of the following array accesses, give
the vector f and the matrix F that describe them. Assume that the vector of indexes i is i, j ,
. . . , and that all loop indexes have affine limits.
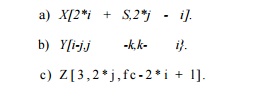
Related Topics