Array Data-Dependence Analysis

Array Data-Dependence Analysis

1 Definition of Data Dependence of Array Accesses

2 Integer Linear Programming

3 The GCD Test

4 Heuristics for Solving Integer Linear Programs

5 Solving General Integer Linear Programs

6 Summary

7 Exercises for Section 11.6

Parallelization or locality optimizations frequently reorder the operations ex-ecuted in the original program. As with all optimizations, operations can be reordered only if the reordering does not change the program's output. Since we cannot, in general, understand deeply what a program does, code optimization generally adopts a simpler, conservative test for when we can be sure that the program output is not affected: we check that the operations on any memory location are done in the same order in the original and modified programs. In the present study, we focus on array accesses, so the array elements are the memory locations of concern.

Two accesses, whether read or write, are clearly independent (can be re-ordered) if they refer to two different locations. In addition, read operations do not change the memory state and therefore are also independent. Following Section 11.5, we say that two accesses are data dependent if they refer to the same memory location and at least one of them is a write operation. To be sure that the modified program does the same as the original, the relative execu-tion ordering between every pair of data-dependent operations in the original program must be preserved in the new program.

Recall from Section 10.2.1 that there are three flavors of data dependence:

2. Antidependence, where a read is followed by a write to the same location.

3.  Output dependence,  which is two writes to the same location.

In the discussion above, data dependence is defined for dynamic accesses. We say that a static access in a program depends on another as long as there exists a dynamic instance of the first access that depends on some instance of the second.⁵

It is easy to see how data dependence can be used in parallelization. For example, if no data dependences are found in the accesses of a loop, we can easily assign each iteration to a different processor. Section 11.7 discusses how we use this information systematically in parallelization.

1. Definition of Data Dependence of Array Accesses

Let us consider two static accesses to the same array in possibly different loops.

The first is represented by access function and bounds T = (F,f, B , b ) and is in a d-deep loop nest; the second is represented by T' = ( F ' , f ,B',b') and is in a rf'-deep loop nest. These accesses are data dependent if

 1. At least one of them is a write reference and

 2. There exist vectors i in Zd and i' in Zd' such that

(a)                     Bi > 0,

(b)                     B'i' > 0, and

(c)                      Fi + f = F'i' + f.

Since a static access normally embodies many dynamic accesses, it is also meaningful to ask if its dynamic accesses may refer to the same memory loca-tion. To search for dependencies between instances of the same static access, we assume T — T' and augment the definition above with the additional constraint that i ^ i' to rule out the trivial solution.

Example 1 1 . 2 9 :  Consider the following 1-deep loop nest:

for (i = 1;  i < 10;  i++) {

Z[i]  =  Z[i-1];

}

This loop has two accesses: Z[i - 1] and Z[i}; the first is a read reference and the second a write. To find all the data dependences in this program, we need to check if the write reference shares a dependence with itself and with the read reference:

1. Data dependence between Z[i - 1] and Z[i]. Except for the first iteration, each iteration reads the value written in the previous iteration. Mathe matically, we know that there is a dependence because there exist integers i and i' such that

There are nine solutions to the above system of constraints: (i = 2, %' — 1), (i = 3,z' = 2), and so forth.

2. Data dependence between Z[i] and itse//. It is easy to see that different iterations in the loop write to different locations; that is, there are no data dependencies among the instances of the write reference Z[i]. Math-ematically, we know that there does not exist a dependence because there do not exist integers i and i' satisfying

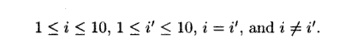
Notice that the third condition, i = i', comes from the requirement that Z[i] and Z[i'] are the same memory location The contradictory fourth condition, i =!i', comes from the requirement that the dependence be nontrivial — between different dynamic accesses.

 It  is  not necessary to  consider data dependences between the  read reference Z[i — 1] and itself because any two read accesses are independent.

2. Integer Linear Programming

Data dependence requires finding whether there exist integers that satisfy a system consisting of equalities and inequalities. The equalities are derived from the matrices and vectors representing the accesses; the inequalities are derived from the loop bounds. Equalities can be expressed as inequalities: an equality x — y can be replaced by two inequalities, x > y and y > x.

Thus, data dependence may be phrased as a search for integer solutions that satisfy a set of linear inequalities, which is precisely the well-known problem of integer linear programming. Integer linear programming is an NP-complete problem. While no polynomial algorithm is known, heuristics have been de-veloped to solve linear programs involving many variables, and they can be quite fast in many cases. Unfortunately, such standard heuristics are inappro-priate for data dependence analysis, where the challenge is to solve many small and simple integer linear programs rather than large complicated integer linear programs.

1. Apply the GCD (Greatest Common Divisor) test, which checks if there is an integer solution to the equalities, using the theory of linear Diophan-tine equations. If there are no integer solutions, then there are no data dependences. Otherwise, we use the equalities to substitute for some of the variables thereby obtaining simpler inequalities.

2.       Use a set of simple heuristics to handle the large numbers of typical in-equalities.

3.       In the rare case where the heuristics do not work, we use a linear integer programming solver that uses a branch-and-bound approach based on Fourier-Motzkin elimination.

3. The GCD Test

The first subproblem is to check for the existence of integer solutions to the equalities. Equations with the stipulation that solutions must be integers are known as Diophantine equations. The following example shows how the issue of integer solutions arises; it also demonstrates that even though many of our examples involve a single loop nest at a time, the data dependence formulation applies to accesses in possibly different loops.

The access Z[2*i] only touches even elements of Z,  while access Z[2 * j + 1] touches only odd elements. Clearly, these two accesses share no data depen-dence regardless of the loop bounds. We can execute iterations in the second loop before the first, or interleave the iterations. This example is not as con-trived as it may look. An example where even and odd numbers are treated differently is an array of complex numbers, where the real and imaginary com-ponents are laid out side by side.

To prove the absence of data dependences in this example,  we reason as follows.  Suppose there were integers i and j such that Z[2 * i] and Z[2 * j + 1] are the same array element.  We get the Diophantine equation

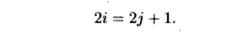
There are no integers i and j that can satisfy the above equation. The proof is that if i is an integer, then 2i is even.  If j is an integer, then 2j is even, so 2j + 1 is odd. No even number is also an odd number.  Therefore, the equation has no integer solutions, and thus there is no dependence between the read and write accesses.

To describe when there is a solution to a linear Diophantine equation, we need the concept of the greatest common  divisor (GCD) of two or more integers. The GCD o f integers 0 1 , a 2 , . . . , a n , denoted gcd(ai, a 2 , • • • , an)y i s the largest integer that evenly divides all these integers. GCD's can be computed efficiently by the well-known Euclidean algorithm (see the box on the subject).

Example 1 1 . 3 1 : gcd(24,36,54) = 6, because 24/6, 36/6, and 54/6 each have remainder 0, yet any integer larger than 6 must leave a nonzero remainder when dividing at least one of 24, 36, and 54. For instance, 12 divides 24 and 36 evenly, but not 54.

The importance of the GCD is in the following theorem.

Theorem 11.32 :  The linear Diophantine equation

has  an  integer  solution  for x1, x2,... ,xn if  and only if gcd(ai, a2,...  , an)  divides c. •    

Example 1 1 . 3 3 : We observed in Example 11.30 that the linear Diophantine equation 2i = 2j + 1 has no solution. We can write this equation as

2i- 2j = 1.

Now gcd(2, —2) = 2, and 2 does not divide 1 evenly. Thus, there is no solution. For another example, consider the equation

24x + 36y + 54z = 30.

Since gcd(24,36,54) = 6, and 30/6 = 5, there is a solution in integers for x, y, and z. One solution is x = —1, y = 0, and z = 1, but there are an infinity of other solutions. •

The first step to the data dependence problem is to use a standard method such as Gaussian elimination to solve the given equalities. Every time a linear equation is constructed, apply Theorem 11.32 to rule out, if possible, the ex-istence of an integer solution. If we can rule out such solutions, then answer "no". Otherwise, we use the solution of the equations to reduce the number of variables in the inequalities.

The Euclidean Algorithm

The Euclidean algorithm for finding gcd(a, b) works as follows. First, as-sume that a and b are positive integers, and a>b. Note that the GCD of negative numbers, or the GCD of a negative and a positive number is the same as the GCD of their absolute values, so we can assume all integers are positive.

If a = b, then gcd(a, b) = a.  If a > b, let c be the remainder of a/b. If c = 0, then b evenly divides a, so gcd(a, b)  = b. Otherwise, compute gcd(6,c); this result will also be gcd(a, b).     

To compute  gcd(ai, a 2 , . . . , an),  for n > 2, use  the Euclidean algorithm to compute  gcd ( a i , a 2 ) = c. Then recursively compute gcd ( c , a 3 , a 4 , • • •  ,an).      

Looking at each equality by itself, it appears there might be a solution. For the  first  equality,  gcd(l, - 2 , 1 ) = 1 divides  0, and for the  second  equality, gcd(3,2,1) =  1 divides 5. However, if we use the first equality to solve for z = 2y — x and substitute for z in the second equality, we get 2x + Ay = 5.

This Diophantine equation has no solution, since gcd(2,4) = 2 does not divide 5 evenly. •

4. Heuristics for Solving Integer Linear Programs

The data dependence problem requires many simple integer linear programs be solved. We now discuss several techniques to handle simple inequalities and a technique to take advantage of the similarity found in data dependence analysis.

Independent - Variables  Test

Many of the integer linear programs from data dependence consist of inequalities that involve only one unknown. The programs can be solved simply by testing if there are integers between the constant upper bounds and constant lower bounds independently.

Example 11 . 35 :  Consider the nested loop

for (i = 0;  i <= 10;  i++)

for (j = 0; j <= 10; j++)

Z[i,j] = Z[j+10,i+9]

To find if there is a data dependence between Z[i, j] and Z[j +10, i + 9], we ask if there exist integers i, j, i', and j' such that

The GCD test, applied to the two equalities above, will determine that there may be an integer solution. The integer solutions to the equalities are expressed by

for any integers t1 and t₂. Substituting the variables t1 and t₂ into the linear inequalities, we get

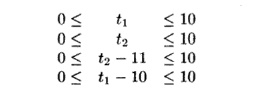
Thus, combining the lower bounds from the last two inequalities with the upper bounds from the first two, we deduce

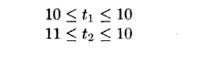
Since the lower bound on t₂ is greater than its upper bound, there is no integer solution, and hence no data dependence. This example shows that even if there are equalities involving several variables, the GCD test may still create linear inequalities that involve one variable at a time. •

Acyclic  Test

Another simple heuristic is to find if there exists a variable that is bounded below or above by a constant. In certain circumstances, we can safely replace the variable by the constant; the simplified inequalities have a solution if and only if the original inequalities have a solution. Specifically, suppose every lower bound on vi is of the form

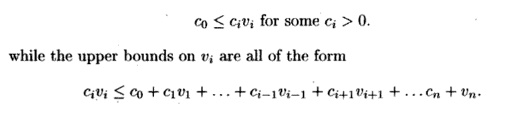
where c1, cx,... , c«  are all nonnegative.  Then we can replace variable Vi  by its smallest possible integer value.  If there is no such lower bound, we simply replace vi with — oo. Similarly, if every constraint involving V{ can be expressed in the two forms above,  but with the directions of the inequalities reversed, then we can replace variable V{ with the largest possible integer value, or by oo if there is no constant upper bound.  This step can be repeated to simplify the inequalities and in some cases determine if there is a solution.

Example 1 1 . 3 6 : Consider the following inequalities:

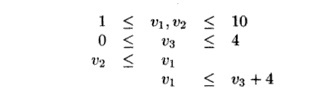
Variable v1 is bounded from below by v2 and from above by v3.  However, v2 is bounded from below only by the constant 1, and v3 is bounded from above only by the constant 4. Thus, replacing v2 by 1 and v3 by 4 in the inequalities, we obtain

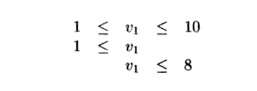
which can now be solved easily with the independent-variables test.

The  Loop - Residue  Test

Let us now consider the case where every variable is bounded from below and above by other variables. It is commonly the case in data dependence analysis that constraints have the form Vi < Vj+c, which can be solved using a simplified version of the loop-residue test due to Shostack. A set of these constraints can be represented by a directed graph whose nodes are labeled with variables. There is an edge from Vi to Vj labeled c whenever there is a constraint Vi < Vj + c.

We define the weight of a path to be the sum of the labels of all the edges along the path. Each path in the graph represents a combination of the con-straints in the system. That is, we can infer that v < v' + c whenever there exists a path from v to v' with weight c. A cycle in the graph with weight c represents the constraint v < v + c for each node v on the cycle. If we can find a negatively weighted cycle in the graph, then we can infer v < v, which is impossible. In this case, we can conclude that there is no solution and thus no dependence.

We can also incorporate into the loop-residue test constraints of the form c < v and v < c for variable v and constant c. We introduce into the system of inequalities a new dummy variable vo, which is added to each constant upper and lower bound. Of course, v₀ must have value 0, but since the loop-residue test only looks for cycles, the actual values of the variables never becomes significant. To handle constant bounds, we replace

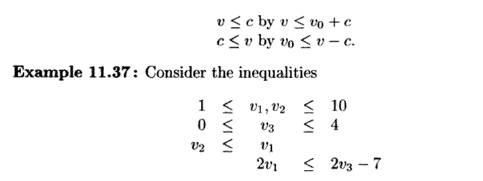
The constant upper and lower bounds on v1 become VQ <v1 — l and v1 < i>o + 10;

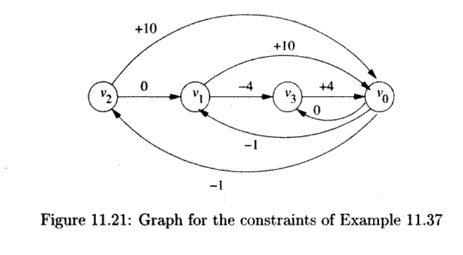
the constant bounds on v2    and v3    are handled similarly.  Then, converting the last constraint to v1 < v3   — 4, we can create the graph shown in Fig.  11.21. The  cycle  v1,v3,Vo,v1 has  weight  — 1,  so  there  is  no  solution  to  this  set  of inequalities.

Memoization

Often, similar data dependence problems are solved repeatedly, because simple access patterns are repeated throughout the program. One important technique to speed up data dependence processing is to use memoization. Memoization tabulates the results to the problems as they are generated. The table of stored solutions is consulted as each problem is presented; the problem needs to be solved only if the result to the problem cannot be found in the table.

5. Solving General Integer Linear Programs

We now describe a general approach to solving the integer linear programming problem. The problem is NP-complete; our algorithm uses a branch-and-bound approach that can take an exponential amount of time in the worst case. How-ever, it is rare that the heuristics of Section 11.6.4 cannot resolve the problem, and even if we do need to apply the algorithm of this section, it seldom needs to perform the branch-and-bound step.

The approach is to first check for the existence of rational solutions to the inequalities. This problem is the classical linear-programming problem. If there is no rational solution to the inequalities, then the regions of data touched by the accesses in question do not overlap, and there surely is no data dependence. If there is a rational solution, we first try to prove that there is an integer solution, which is commonly the case. Failing that, we then split the polyhedron bounded by the inequalities into two smaller problems and recurse.

The  elements  touched by access  Z[i]  are Z [ l ] , . . . ,Z[9], while the  elements touched by  Z[i + 10] are Z [ l l ] , . . . , Z[19]. The ranges do not overlap and therefore there are no data dependences. More formally, we need to show that there are no two dynamic accesses i and i', with 1 < i < 9, 1 < i' < 9, and i = %' + 10. If there were such integers i and i', then we could substitute i' + 10  for i and get the four constraints on i':  1 < i' < 9 and 1 < i' +10 < 9.  However, i' + 10 < 9 implies i' < — 1, which contradicts 1 < i'.  Thus, no such integers i and %' exist.

Algorithm 11.39 describes how to determine if an integer solution can be found for a set of linear inequalities based on the Fourier-Motzkin elimination algorithm.

Algorithm 11.39 :  Branch-and-bound solution to integer linear programming problems. 

INPUT :  A convex polyhedron  Sn    over variables vi,...  ,vn.

OUTPUT : "yes" if Sn   has an integer solution, "no" otherwise.

METHOD : The algorithm is shown in Fig. 11.22.

Lines (1) through (3) attempt to find a rational solution to the inequalities.

If there no rational solution, there is no integer solution. If a rational solution is found, this means that the inequalities define a nonempty polyhedron. It is relatively rare for such a polyhedron not to include any integer solutions — for that to happen, the polyhedron must be relatively thin along some dimension and fit between integer points.

Thus, lines (4) through (9) try to check quickly if there is an integer solution. Each step of the Fourier-Motzkin elimination algorithm produces a polyhedron with one fewer dimension than the previous one. We consider the polyhedra in reverse order. We start with the polyhedron with one variable and assign to that variable an integer solution roughly in the middle of the range of possible values if possible. We then substitute the value for the variable in all other polyhedra, decreasing their unknown variables by one. We repeat the same process until

we have processed all the polyhedra, in which case an integer solution is found, or we have found a variable for which there is no integer solution.

If we cannot find an integer value for even the first variable, there is no integer solution (line 10). Otherwise, all we know is that there is no integer solution including the combination of specific integers we have picked so far, and the result is inconclusive. Lines (11) through (13) represent the branch-and-bound step. If variable Vi is found to have a rational but not integer solution, we split the polyhedron into two with the first requiring that Vi must be an integer smaller than the rational solution found, and the second requiring that Vi must be an integer greater than the rational solution found. If neither has a solution, then there is no dependence.

6. Summary

We have shown that essential pieces of information that a compiler can glean from array references are equivalent to certain standard mathematical concepts. Given an access function T — (F, f, B, b):

1. The dimension of the data region accessed is given by the rank of the matrix F. The dimension of the space of accesses to the same location is given by the nullity of F. Iterations whose differences belong to the null space of F refer to the same array elements.

2.              Iterations that share self-temporal reuse of an access are separated by vectors in the null space of F. Self-spatial reuse can be computed similarly by asking when two iterations use the same row, rather than the same

element. Two accesses Fix + fi and F i ₂ + f₂ share easily exploitable locality along the d direction, if d is the particular solution to the equation Fd = (fi - f₂ ). In particular, if d is the direction corresponding to the innermost loop, i.e., the vector [ 0 , 0 , . . . , 0,1], then there is spatial locality if the array is stored in row-major form.

3.              The data dependence problem — whether two references can refer to the same location — is equivalent to integer linear programming. Two access functions share a data dependence if there are integer-valued vectors i and i' such that Bi > 0, B'i' > 0, and Fi + f = F'i' + f.

7. Exercises for Section 11.6

Exercise 1 1 . 6 . 1 :  Find the GCD's of the following sets of integers:

a)              {16,24,56}.

b)               { - 45,105,240,} .

!          c)  {84,105,180,315,350}.