Chapter: Fundamentals of Database Systems : Query Processing and Optimization, and Database Tuning : Algorithms for Query Processing and Optimization
Multiple Relation Queries and JOIN Ordering
Multiple
Relation Queries and JOIN Ordering
The algebraic transformation rules in Section
19.7.2 include a commutative rule and an associative rule for the join
operation. With these rules, many equivalent join expressions can be produced.
As a result, the number of alternative query trees grows very rapidly as the
number of joins in a query increases. A query that joins n relations will often have n
− 1 join operations, and hence can have a large
number of different join orders. Estimating the cost of every possible join
tree for a query with a large number of joins will require a substantial amount
of time by the query opti-mizer. Hence, some pruning of the possible query
trees is needed. Query optimizers typically limit the structure of a (join)
query tree to that of left-deep (or right-deep) trees. A left-deep tree is a binary tree in which the right child of each
nonleaf node is always a base relation. The optimizer would choose the
particular left-deep tree with the lowest estimated cost. Two examples of
left-deep trees are shown in Figure 19.7. (Note that the trees in Figure 19.5
are also left-deep trees.)
With left-deep trees, the right child is
considered to be the inner relation when executing a nested-loop join, or the
probing relation when executing a single-loop join. One advantage of left-deep
(or right-deep) trees is that they are amenable to pipelining, as discussed in
Section 19.6. For instance, consider the first left-deep tree in Figure 19.7
and assume that the join algorithm is the single-loop method; in this case, a
disk page of tuples of the outer relation is used to probe the inner relation
for
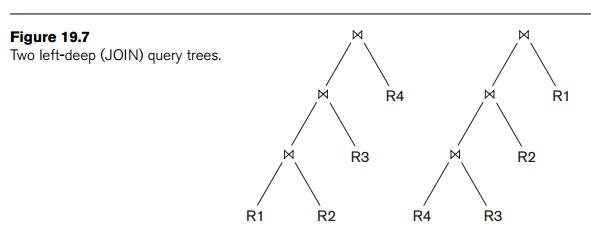
matching tuples. As resulting tuples (records)
are produced from the join of R1 and R2, they can be used to probe R3 to locate
their matching records for joining. Likewise, as resulting tuples are produced
from this join, they could be used to probe R4. Another advantage of left-deep
(or right-deep) trees is that having a base relation as one of the inputs of
each join allows the optimizer to utilize any access paths on that relation
that may be useful in executing the join.
If materialization is used instead of
pipelining (see Sections 19.6 and 19.7.3), the join results could be
materialized and stored as temporary relations. The key idea from the
optimizer’s standpoint with respect to join ordering is to find an ordering
that will reduce the size of the temporary results, since the temporary results
(pipelined or materialized) are used by subsequent operators and hence affect
the execution cost of those operators.
Related Topics