Chapter: Fundamentals of Database Systems : Query Processing and Optimization, and Database Tuning : Algorithms for Query Processing and Optimization
Implementing the JOIN Operation and Algorithms
Implementing the JOIN Operation
The JOIN operation is one of the most time-consuming operations in query
processing. Many of the join operations encountered in queries are of the EQUIJOIN and NATURAL JOIN varieties, so we consider just these two here
since we are only giving an overview of query processing and optimization. For
the remainder of this chapter, the term join
refers to an EQUIJOIN (or NATURAL JOIN).
There
are many possible ways to implement a two-way
join, which is a join on two files. Joins involving more than two files are
called multiway joins. The number of
possible ways to execute multiway joins grows very rapidly. In this section we
dis-cuss techniques for implementing only
two-way joins. To illustrate our discussion, we refer to the relational
schema in Figure 3.5 once more—specifically, to the EMPLOYEE, DEPARTMENT, and PROJECT relations. The algorithms we discuss next are for a join operation of the form:
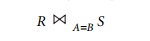
where A
and B are the join attributes, which should be domain-compatible attributes of R and S, respectively. The methods we discuss can be extended to more
general forms of join. We illustrate four of the most common techniques for
performing such a join, using the following sample operations:
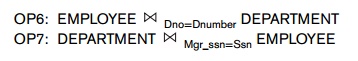
Methods for Implementing Joins.
J1—Nested-loop join (or nested-block join). This is the default (brute force) algorithm, as it does not require any special access paths on either file in the join. For each record t in R (outer loop), retrieve every record s from S (inner loop) and test whether the two records satisfy the join condition t[A] = s[B].
J2—Single-loop join (using an access structure
to retrieve the matching records). If an index (or hash key) exists for one of the two join
attributes— say, attribute B of file S—retrieve each record t
in R (loop over file R), and then use the access structure
(such as an index or a hash key) to retrieve directly all matching records s from S that satisfy s[B] = t[A].
J3—Sort-merge
join. If the records of R and S are physically sorted (ordered) by value of
the join attributes A and B, respectively, we can implement the
join in the most efficient way possible. Both files are scanned concurrently in
order of the join attributes, matching the records that have the same values
for A and B. If the files are not sorted, they may be sorted first by using
external sorting (see Section 19.2).
In this method, pairs of file blocks are copied into memory buffers in order
and the records of each file are scanned only once each for matching with the
other file—unless both A and B are nonkey attributes, in which case
the method needs to be modified slightly. A sketch of the sort-merge join
algorithm is given in Figure 19.3(a). We use R(i) to refer to the ith record in file R. A variation of the sort-merge join can be used when secondary
indexes exist on both join attributes. The indexes provide the ability to
access (scan) the records in order of the join attributes, but the records
themselves are physically scattered all over the file blocks, so this method
may be quite inefficient, as every record access may involve accessing a
different disk block.
J4—Partition-hash join. The records of files R and S
are partitioned into smaller
files. The partitioning of each file is done using the same hashing function h on the join attribute A of R
(for partitioning file R) and B of S (for partitioning file S). First, a
single pass through the file with fewer records (say, R) hashes its records to the various partitions of R; this is
called the partitioning phase, since the records of R are partitioned into the hash buck-ets. In the simplest case, we
assume that the smaller file can fit entirely in main memory after it is
partitioned, so that the partitioned subfiles of R are all kept in main memory. The collection of records with the
same value of h(A) are placed in the same partition, which is a hash bucket in a hash table in main memory. In the second phase, called the probing phase, a single pass through
the other file (S) then hashes each
of its records using the same hash function h(B) to probe the appropriate bucket, and that record is combined with all
matching records from R in that
bucket. This simplified description of partition-hash join assumes that the
smaller of the two files fits entirely
into memory buckets after the
first phase. We will discuss the general case of partition-hash join that does not require this assumption below.
In practice, techniques J1 to J4 are implemented by accessing whole disk blocks of a file, rather than
individual records. Depending on the available number of buffers in memory, the
number of blocks read in from the file can be adjusted.
How Buffer Space and Choice
of Outer-Loop File Affect Performance of Nested-Loop Join. The buffer space available has an important
effect on some of the join algorithms. First, let us consider the
nested-loop approach (J1). Looking again at the operation OP6 above, assume that the number of buffers available in main memory
for implementing the join is nB
= 7 blocks (buffers). Recall that we assume that each memory buffer is the same
size as one disk block. For illustration, assume that the DEPARTMENT file consists of rD
= 50 records stored in bD
= 10 disk blocks and that the EMPLOYEE file consists of rE = 6000 records stored in bE = 2000 disk blocks. It is advantageous to read as
many blocks as possible at a time into memory from the file whose records are
used for the outer loop (that is, nB
− 2 blocks). The algorithm can then read one block at a time for the
inner-loop file and use its records to probe
(that is, search) the outer-loop blocks that are currently in main memory for
matching records. This reduces the total number of block accesses. An extra
buffer in main memory is needed to contain the resulting records after they are
joined, and the contents of this result buffer can be appended to the result file—the disk file that will
contain the join result—whenever it is filled. This result buffer block then is reused to hold additional join result
records.
Figure 19.3
Implementing JOIN, PROJECT, UNION,
INTERSECTION, and SET DIFFERENCE by using sort-merge, where R has n tuples and S has m tuples. (a) Implementing the
opera-tion T ← R >< A=BS. (b) Implementing the operation T ← π<attribute list>(R).
(a) sort
the tuples in R on attribute A; (* assume R
has n tuples (records) *)
sort the
tuples in S on attribute B; (* assume S
has m tuples (records) *)
set i ← 1, j ← 1;
while (i ≤ n) and ( j ≤ m)
do { if R( i
) [A] > S( j ) [B]
then set j
← j + 1
elseif R( i
) [A] < S( j ) [B]
then set i
← i + 1
else { (* R(
i ) [A] = S( j ) [B],
so we output a matched tuple *)
output
the combined tuple <R( i ) , S( j ) > to T;
(*
output other tuples that match R(i), if any *) set I ← j + 1;
while (l
≤ m) and (R( i ) [A] = S(
l ) [B])
do {
output the combined tuple <R( i ) , S( l ) > to T; set l ← l + 1
}
(*
output other tuples that match S(j), if any *) set k ← i + 1;
while (k ≤ n) and (R( k ) [A] = S(
j ) [B])
do {
output the combined tuple <R( k ) , S( j ) > to T; set k ← k + 1
}
set i ← k,
j ← l
}
}
(b) create
a tuple t[<attribute list>] in T for each tuple t in R;
(* T contains the projection results before duplicate elimination *)
if
<attribute list> includes a key of R
then T ← T
else { sort the tuples in T ;
set i ← 1, j ← 2;
while i f n
do { output
the tuple T [ i
] to T;
while T
[ i ] = T [ j ] and j ≤ n do
j ← j + 1; (* eliminate duplicates *)
i ← j; j ←
i + 1
}
}
Implementing JOIN, PROJECT, UNION,
INTERSECTION, and SET DIFFERENCE by using sort-merge, where R has n tuples and S has m tuples. (c) Implementing the operation
T ← R
∪ S. (d)
Implementing the operation T ← R ∩
S. (e) Implementing the operation T ← R – S.
sort the tuples in R and S using the same
unique sort attributes; set i ← 1, j ← 1;
while (i ≤ n) and (j ≤ m) do { if R( i ) > S( j
)
then { output
S( j ) to T;
set j ← j + 1
}
elseif
R( i ) < S( j )
then { output
R( i ) to T;
set i ← i + 1
}
else set j ← j + 1 (* R(i ) = S ( j ) , so we skip one of the duplicate
tuples *)
}
if (i
≤ n)
then add tuples R( i ) to R(n) to T; if (j ≤ m)
then add tuples S( j ) to S(m) to T;
sort the tuples in R and S using the same
unique sort attributes; set i ← 1, j ← 1;
while ( i ≤ n) and ( j ≤ m) do { if R( i ) > S( j
)
then set j
← j + 1
elseif R( i
) < S( j )
then set i
← i + 1
else { output R( j
) to T; (* R(
i ) =S( j ) , so we output the
tuple *)
set i ← i
+ 1, j ← j + 1
}
}
sort the tuples in R and S using the same
unique sort attributes; set i ← 1, j ← 1;
while (i f n)
and ( j ≤ m)
do { if R( i ) > S(j)
then set j
← j + 1
elseif R(i)
< S( j )
then
{ output R( i ) to T; (* R( i ) has no matching S( j ) , so
output R( i ) *)
set i ←
i + 1
}
else set i ← i + 1, j ← j + 1
}
if (i ≤
n) then add tuples R( i ) to R( n ) to T;
In the nested-loop join, it makes a difference
which file is chosen for the outer loop and which for the inner loop. If EMPLOYEE is used for the outer loop, each block of EMPLOYEE is read once, and the entire
DEPARTMENT file (each of its blocks) is
read once for each time we
read in (nB – 2) blocks of
the EMPLOYEE file. We get the follow-ing formulas for the number of disk blocks
that are read from disk to main memory:
Total number of blocks accessed (read) for
outer-loop file = bE
Number of times (nB − 2) blocks of outer file are loaded into main memory = bE/(nB – 2)
Total number of blocks accessed (read) for
inner-loop file = bD *
bE/(nB – 2) Hence, we get the following total number of
block read accesses:
bE
+ ( bE/(nB – 2) *
bD) = 2000 + ( (2000/5)
* 10) = 6000 block accesses
On the other hand, if we use the DEPARTMENT records in the outer loop, by symme-try we get the following total
number of block accesses:
bD
+ ( bD/(nB – 2) *
bE) = 10 + ( (10/5)
* 2000) = 4010 block accesses
The join algorithm uses a buffer to hold the
joined records of the result file. Once the buffer is filled, it is written to
disk and its contents are appended to the result file, and then refilled with
join result records.10
If the result file of the join operation has bRES disk blocks, each block
is written once to disk, so an additional bRES
block accesses (writes) should be added to the preced-ing formulas in order to
estimate the total cost of the join operation. The same holds for the formulas
developed later for other join algorithms. As this example shows, it is
advantageous to use the file with fewer
blocks as the outer-loop file in the nested-loop join.
How the Join Selection Factor Affects Join
Performance. Another factor that affects the performance of a join, particularly the single-loop
method J2, is the frac-tion of records in one file that will be joined with
records in the other file. We call this the join selection factor11 of a file with respect to an
equijoin condition with another file. This factor depends on the particular
equijoin condition between the two files. To illustrate this, consider the
operation OP7, which joins each DEPARTMENT record with the
EMPLOYEE record for the manager of
that depart-ment. Here, each DEPARTMENT record (there are 50 such records in our
example) will be joined with a single
EMPLOYEE record, but many EMPLOYEE records (the 5,950 of them that do not manage
a department) will not be joined with any record from DEPARTMENT.
Suppose that secondary indexes exist on both
the attributes Ssn of EMPLOYEE and Mgr_ssn of
DEPARTMENT, with the number of index
levels xSsn = 4 and xMgr_ssn= 2, respectively. We have two options for
implementing method J2. The first retrieves each EMPLOYEE record and then uses the index on Mgr_ssn of DEPARTMENT to find a matching DEPARTMENT record. In this case, no matching record will be found for
employees who do not manage a department. The number of block accesses for this
case is approximately:
bE
+ (rE
* (xMgr_ssn + 1)) = 2000 + (6000 * 3) = 20,000
block accesses
The second option retrieves each DEPARTMENT record and then uses the index on Ssn
of
EMPLOYEE to find a matching manager EMPLOYEE record. In this case, every
DEPARTMENT record will have one matching EMPLOYEE record. The number of block accesses for this case is approximately:
bD
+ (rD
* (xSsn + 1)) = 10 + (50 * 5) = 260
block accesses
The second option is more efficient because the join selection factor of
DEPARTMENT with respect to the join condition Ssn = Mgr_ssn is 1 (every record in
DEPARTMENT will be joined), whereas the join selection factor of EMPLOYEE with respect to the same join condition is
(50/6000), or 0.008 (only 0.8 percent of the records in EMPLOYEE will be joined). For method J2, either the smaller file or the
file that has a match for every record (that is, the file with the high join
selection factor) should be used in the (single) join loop. It is also
possible to create an index specifically for performing the join operation if
one does not already exist.
The sort-merge join J3 is quite efficient if
both files are already sorted by their join attribute. Only a single pass is
made through each file. Hence, the number of blocks accessed is equal to the
sum of the numbers of blocks in both files. For this method, both OP6 and OP7 would need bE
+ bD = 2000 + 10 = 2010
block accesses. However, both files are required to be ordered by the join
attributes; if one or both are not, a sorted copy of each file must be created
specifically for performing the join operation. If we roughly estimate the
cost of sorting an external file by (b
log2b) block
accesses, and if both files need to be sorted,
the total cost of a sort-merge join can be estimated by (bE + bD
+ bE log2bE + bD log2bD).12
General Case for Partition-Hash Join. The hash-join method J4 is also quite efficient. In this case only a single pass is made through each
file, whether or not the files are ordered. If the hash table for the smaller
of the two files can be kept entirely in main memory after hashing
(partitioning) on its join attribute, the implementation is straightforward.
If, however, the partitions of both files must be stored on disk, the method
becomes more complex, and a number of variations to improve the efficiency have
been proposed. We discuss two techniques: the general case of partition-hash join and a variation
called hybrid hash-join algorithm,
which has been shown to be quite
efficient.
In the general case of partition-hash join,
each file is first partitioned into M partitions using the same partitioning
hash function on the join attributes. Then, each pair of corresponding
partitions is joined. For example, suppose we are joining relations R and S on the join attributes R.A
and S.B:
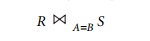
In the partitioning
phase, R is partitioned into the M partitions R1, R2,
..., RM, and S into the M partitions S1, S2, ..., SM. The property of each pair of corresponding partitions Ri, Si
with respect to the join operation is that records in Ri only need to be
joined with records in Si, and vice versa. This
property is ensured by using the same
hash function to partition both files on their join attributes—attribute A for R and attribute B for S. The minimum number of in-memory buffers needed for the partitioning phase is M
+ 1. Each of the files R and S are partitioned separately.
During partitioning of a file, M
in-memory buffers are allocated to store the records that hash to each partition,
and one additional buffer is needed to hold one block at a time of the input
file being partitioned. Whenever the in-memory buffer for a par-tition gets
filled, its contents are appended to a disk
subfile that stores the partition. The partitioning phase has two iterations. After the first
iteration, the first file R is
partitioned into the subfiles R1,
R2, ..., RM, where all the records
that hashed to the same buffer are in the same partition. After the second
iteration, the second file S is
similarly partitioned.
In the second phase, called the joining or probing phase, M iterations
are needed. During iteration i, two
corresponding partitions Ri
and Si are joined. The
minimum number of buffers needed for iteration i is the number of blocks in the smaller of the two partitions, say
Ri, plus two additional
buffers. If we use a nested-loop join during iteration i, the records from the smaller of the two partitions Ri are copied into memory
buffers; then all blocks from the other partition Si are read—one at a time—and each record is used to probe (that is, search) partition Ri for matching record(s).
Any matching records are joined and written into the result file. To improve
the efficiency of in-memory probing, it is common to use an in-memory hash table for storing the records in partition Ri by using a
different hash function from the
partitioning hash function.
We can approximate the cost of this partition
hash-join as 3 * (bR
+ bS) + bRES for our example, since
each record is read once and written back to disk once during the
partitioning phase. During the joining
(probing) phase, each record is read a second time to perform the join. The main difficulty of this algorithm is to
ensure that the partitioning hash function is uniform—that is, the partition sizes are nearly equal in size. If
the partitioning function is skewed
(nonuniform), then some partitions may be too large to fit in the available
memory space for the second joining phase.
Notice that if the available in-memory buffer
space nB > (bR + 2), where bR is the number of blocks
for the smaller of the two files
being joined, say R, then there is no
reason to do partitioning since in this case the join can be performed entirely
in memory using some variation of the nested-loop join based on hashing and
probing.
For illustration, assume we are performing the
join operation OP6, repeated below
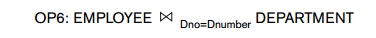
In this example, the smaller file is the DEPARTMENT file; hence, if the number of available memory buffers nB > (bD + 2), the whole DEPARTMENT file can be read into main memory and
organized into a hash table on the join attribute. Each EMPLOYEE block is then read into a buffer, and each EMPLOYEE record in the buffer is hashed on its join attribute and is used to probe the corresponding in-memory bucket
in the DEPARTMENT hash table. If a matching record is found, the records are joined,
and the result record(s) are written to the result buffer and eventually to the
result file on disk. The cost in terms of block accesses is hence (bD + bE), plus bRES—the
cost of writing the result file.
Hybrid Hash-Join. The hybrid
hash-join algorithm is a variation of partition hash-join, where the joining
phase for one of the partitions is
included in the partitioning phase.
To illustrate this, let us assume that the size of a memory buffer is one disk block; that nB such buffers are available; and that the partitioning
hash function used is h(K) = K
mod M, so that M partitions are being created, where M < nB. For
illustration, assume we are performing the join operation OP6. In the first pass of the partitioning phase, when the
hybrid hash-join algorithm is partitioning
the smaller of the two files (DEPARTMENT in OP6), the algorithm divides the buffer space among
the M partitions such that all the
blocks of the first partition of DEPARTMENT completely reside in main memory. For each of the other partitions, only a single in-memory buffer—whose size is one disk block—is
allocated; the remainder of the partition is written to disk as in the regular
partition-hash join. Hence, at the end of the first pass of the partitioning phase, the first partition of DEPARTMENT resides wholly in main memory, whereas each of the other partitions of DEPARTMENT resides in a disk subfile.
For the second pass of the partitioning phase,
the records of the second file being joined—the larger file, EMPLOYEE in OP6—are being partitioned. If a record hashes to
the first partition, it is joined with
the matching record in DEPARTMENT and the joined records are written to the
result buffer (and eventually to disk). If an EMPLOYEE
record hashes to a partition other than the
first, it is partitioned nor-mally and stored to disk. Hence, at the end of the
second pass of the partitioning phase, all records that hash to the first
partition have been joined. At this point, there are M − 1 pairs of partitions on disk. Therefore, during the second joining or probing phase, M
− 1 iterations are needed
instead of M. The goal is to join
as many records during the
partitioning phase so as to save the cost of storing those records on disk and
then rereading them a second time during the joining phase.
Related Topics