Chapter: Operations Research: An Introduction : Network Models
Minimal Spanning Tree Algorithm
MINIMAL SPANNING TREE ALGORITHM
The
minimal spanning tree algorithm deals with linking the nodes of a network,
directly or indirectly, using the shortest total length of connecting branches.
A typical applica-tion occurs in the construction of paved roads that link
several rural towns. The road between two towns may pass through one or more
other towns. The most economical design of the road system calls for minimizing
the total miles of paved roads, a result that is achieved by implementing the
minimal spanning tree algorithm.
The steps
of the procedure are given as follows. Let N
= {I, 2, ….,n} be the set of nodes of
the network and define

Example 6.2-1
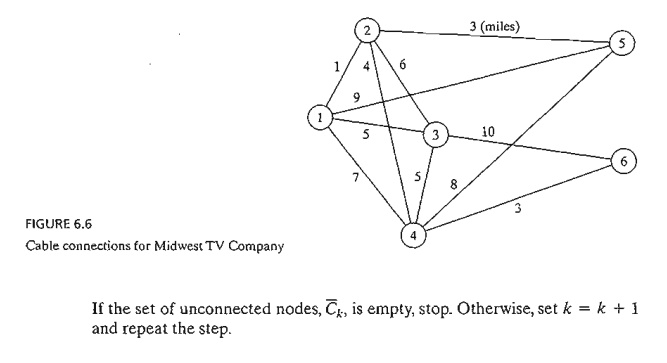
Midwest
TV Cable Company is in the process of providing cable service to five new housing
development areas. Figure 6.6 depicts possible TV linkages among the five
areas. The cable miles are shown on each arc. Determine the most economical
cable network.
The
algorithm starts at node 1 (any other node will do as well), which gives
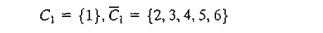
The
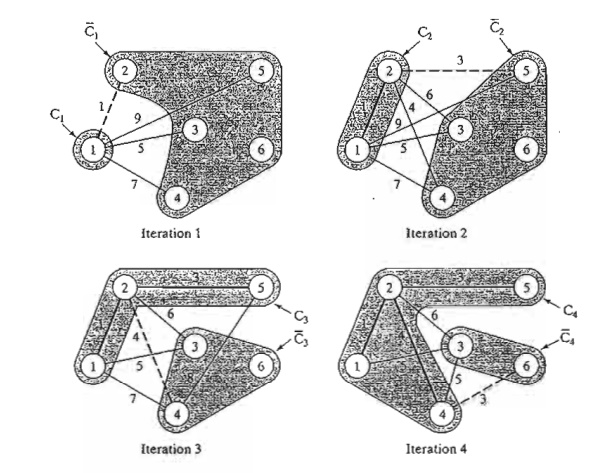
iterations of the algorithm are summarized in Figure 6.7. The thin arcs provide
all the candidate links between C and Bar(C). The
thick branches represent the permanent links between the nodes of the connected
set c: and the dashed branch represents
the new (permanent) link added at each iteration. For example, in iteration 1,
branch (1,2) is the shortest link (= 1 mile)
among all the candidate branches from node 1 to nodes 2,3,4,5, and 6 of the
unconnected set Bar(C1).
Hence, link (1,2) is made permanent and j*
= 2, which yields
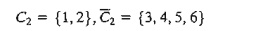
The
solution is given by the minimal spanning tree shown in iteration 6 of Figure
6.7. The resulting minimum cable miles needed to provide the desired cable
service are 1 + 3 + 4 + 3 + 5 = 16 miles.

PROBLEM SET
6.2A
1. Solve
Example 6.2-1 starting at node 5 (instead of node 1), and show that the
algorithm produces the same solution.
2. Determine
the minimal spanning tree of the network of Example 6.2-1 under each of the
following separate conditions:
*(a) Nodes
5 and 6 are linked by a 2-mile cable.
(b) Nodes
2 and 5 cannot be linked.
(c) Nodes
2 and 6 are linked by a 4-mile cable.

(d) The
cable between nodes 1 and 2 is 8 miles long.
(e) Nodes
3 and 5 are linked by a 2-mile cable.
(f) Node
2 cannot be linked directly to nodes 3 and 5.
3. In
intermodal transportation, loaded truck trailers are Shipped between railroad
terminals on special flatbed carts. Figure 6.8 shows the location of the main
railroad terminals in the United States and the existing railroad tracks. The
objective is to decide which tracks should be "revitalized" to handle
the intermodal traffic. In particular, the Los Angeles (LA) terminal must be
linked directly to Chicago (CH) to accommodate expected heavy traffic. Other
than that, all the remaining terminals can be linked, directly or indirectly,
such that the total length (in miles) of the selected tracks is minimized.
Determine the segments of the railroad tracks that must be included in the
revitalization program.
4. Figure
6.9 gives the mileage of the feasible links connecting nine offshore natural
gas wellheads with an inshore delivery point. Because wellhead 1 is the closest
to shore, it is equipped with sufficient pumping and storage capacity to pump
the output of the remain-ing eight wells to the delivery point. Determine the
minimum pipeline network that links the wellheads to the delivery point.
*5. In
Figure 6.9 of Problem 4, suppose that the wellheads can be divided into two
groups depending on gas pressure: a high-pressure group that includes wells
2,3,4, and 6, and a low-pressure group that includes wells 5, 7, 8, and 9.
Because of pressure difference, it is not possible to link the wellheads from
the two groups. At the same time, both groups must be connected to the delivery
point through wellhead 1. Determine the minimum pipeline network for this
situation.
6. Electro
produces 15 electronic parts on 10 machines. The company wants to group the machines
into cells designed to minimize the "dissimilarities" among the parts
processed in each cell. A measure of "dissimilarity," dij , among
the parts processed on machines i and
j can be
expressed as
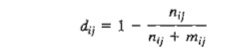
where nij is the
number of parts shared between machines i
and j, and mij is the
number of parts that are used by either machine i or machine j only.

a) Express
the problem as a network model.
b) Show that
the determination of the cells can be based on the minimal spanning tree
solution.
c) For the
data given in the preceding table, construct the two- and three-cell solutions.
Related Topics