CPM AND PERT: PERT Networks

PERT Networks

PERT differs from CPM in that it bases the duration of an activity on three estimates:

a.     Optimistic time, a, which occurs when execution goes extremely welL

b.     Most likely time, m, which occurs when execution is done under nonnal conditions.

c.      Pessimistic time, b, which occurs when execution goes extremely poorly.

The range (a, b) encloses all possible estimates of the duration of an activity. The estimate m lies somewhere in the range (a, b). Based on the estimates, the average duration time, Bar(D), and variance, v, are approximated as:

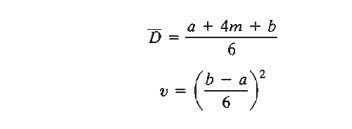
CPM calculations given in Sections 6.5.2 and 6.5.3 may be applied directly, with Bar(D) replacing the single estimate D.

It is possible now to estimate the probability that a node j in the network will occur by a prespecified scheduled time, s_j. Let ej be the earliest occurrence time of node j. Because the durations of the activities leading from the start node to node j are random variables, ej also must be a random variable. Assuming that all the activities in the network are statistically independent, we can determine the mean, E{e_j}, and vari-ance, var{ e_j}, in the following manner. If there is only one path from the start node to node j, then the mean is the sum of expected durations,Bar( D), for all the activities along this path and the variance is the sum of the variances, v, of the same activities. On the other hand, if more than one path leads to node j, then it is necessary first to determine the statistical distribution of the duration of the longest path. This problem is rather difficult because it is equivalent to determining the distribution of the maximum of two or more random variables. A simplifying assumption thus calls for computing the mean and variance, E{e_j} and var{e_j}, as those of the path to node j that has the largest sum of expected activity durations. If two or more paths have the same mean, the one with the largest variance is selected because it reflects the most uncertainty and, hence, leads to a more conservative estimate of probabilities.

Once the mean and variance of the path to node j, E{ ej} and var{ej}, have been computed, the probability that node j will be realized by a preset time s_j is calculated using the following formula:

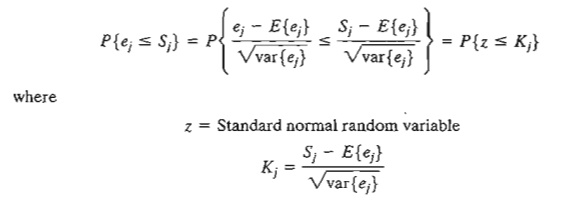
The standard normal variable z has mean 0 and standard deviation 1 (see Section 12.4.4). Justification for the use of the normal distribution is that ej is the sum of independent random variables. According to the central limit theorem (see Section 12.4.4), e_j is approximately normally distributed.

Example 6.5-6

Consider the project of Example 6.5-2. To avoid repeating critical path calculations, the values of a, m, and b in the table below are selected such that Bar(D_ij ) = D_ij for all i and j in Example 6.5-2.

The mean Bar(D_ij) and variance v_ij for the different activities are given in the following table. Note that for a dummy activity (a, m, b) = (0,0,0), hence its mean and variance also equal zero.

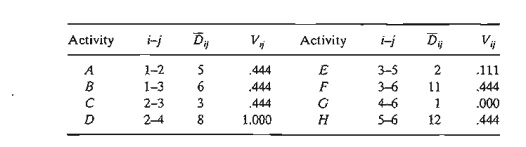
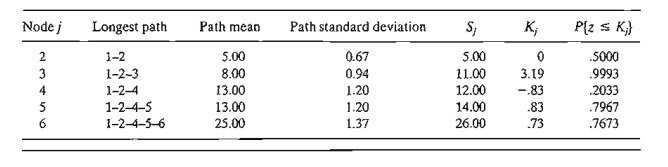
The next table gives the longest path from node 1 to the different nodes, together with their associated mean and standard deviation.

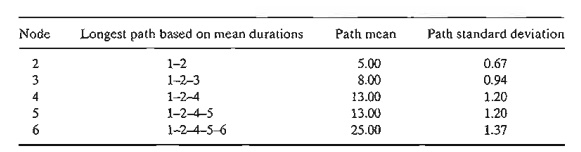
Finally, the following table computes the probability that each node is realized by time s_j specified by the analyst.

PROBLEM SET 6.5E

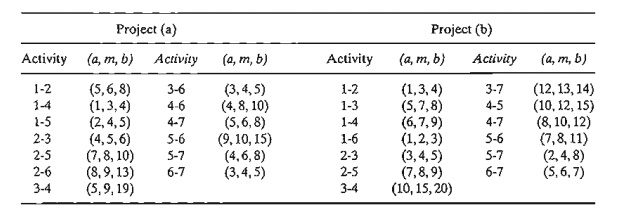
            Consider Problem 2, Set 6.Sb. The estimates (a, m, b) are listed below. Determine the probabilities that the different nodes of the project will be realized without delay.