CPM AND PERT: Construction of the Time Schedule

Construction of the Time Schedule

This section shows how the information obtained from the calculations in Previous Section can be used to develop the time schedule. We recognize that for an activity (i, j), ð_i represents the earliest start time, and Δ_j  represents the latest completion (fine. TIlis means that the interval (ð_{I ,} , Δ_j )  delineates the (maximum) span during which activity (i, j) may be scheduled without delaying the entire project.

Construction of Preliminary Schedule.   The method for constructing a preliminary schedule is illustrated by an example.

Example 6.5-3

Determine the time schedule for the project of Example 6.5-2 (Figure 6.42).

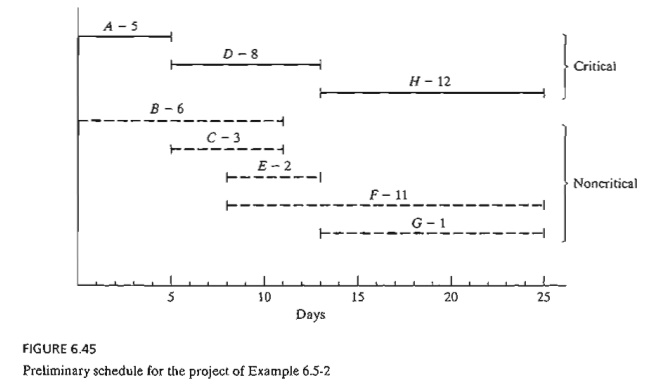
We can get a preliminary time schedule for the different activities of the project by delineating their respective time spans as shown in Figure 6.45. Two observations are in order.

a.     The critical activities (shown by solid lines) must be stacked one right after the other to ensure that the project is completed within its specified 25-day duration.

b.     The noncritical activities (shown by dashed lines) have time spans that are larger than their respective durations, thus allowing slack (or "leeway") in scheduling them within their allotted time intervals.

How should we schedule the noncritical activities within their respective spans? Normally, it is preferable to start each noncritical activity as early as possible. In this manner, slack periods will remain opportunely available at the end of the allotted span where they can be used to absorb unexpected delays in the execution of the activity. It may be necessary, however, to delay the start of a noncritical activity past its earliest start time. For example, in Figure 6.45, suppose that each of the noncritical activities E and F requires the use of a bulldozer, and that only one is available. Scheduling both E and F as early as possible requires two bulldozers between times 8 and 10. We can remove the overlap by starting E at time 8 and pushing the start time of F to somewhere between times 10 and 14.

If all the noncritical activities can be scheduled as early as possible, the resulting schedule automatically is feasible. Otherwise, some precedence relationships may be violated if noncritical activities are delayed past their earliest time. Take for example activities C and E in Figure 6.45. In the project network (Figure 6.42 ), though C must be completed before E, the spans of C and E in Figure 6.45 allow us to schedule C between times 6 and 9, and E between times 8 and 10, which violates the requirement that C precede E. The need for a "red flag" that automatical-ly reveals schedule conflict is thus evident. Such information is provided by computing the floats for the noncritical activities.

Determination of the Floats. Floats are the slack times available within the allotted span of the noncritical activity. The most common are the total float and the free float.

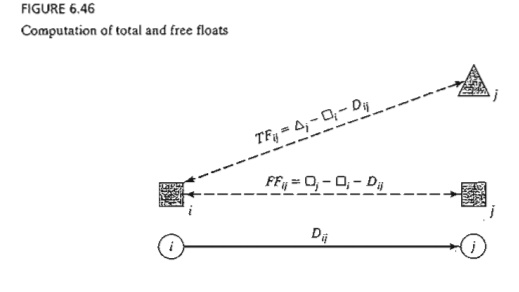
Figure 6.46 gives a convenient summary for computing the total float (TF_ij) and the free float (FF_ij) for an activity (i, j). The total float is the excess of the time span defmed from the earliest occurrence of event i to the latest occurrence of event j over the duration of (i, j)-that is,

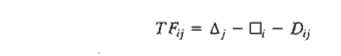
The free float is the excess of the time span defined from the earliest occurrence of event i to the earliest occurrence of event j over the duration of (i, j)-that is,

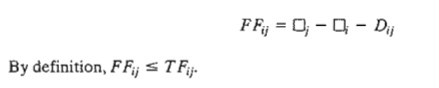
Red-Flagging Rule. For a noncritical activity (i, j)

(a) If F F_ij = T F_ij, then the activity can be scheduled anywhere within its (ð_j,Δ_j ) span without causing schedule conflict.

(b) If F F_ij < T F_ij, then the start of the activity can be delayed by at most F F_ij relative to its earliest start time (ð_i ) without causing schedule conflict. Any delay larger than F F_ij (but not more than T F_ij) must be coupled with an equal delay relative to ð_j in the start time ofall the activities leaving node j.

The implication of the rule is that a noncritical activity (i, j) will be red-flagged if its F F_ij < T F_ij. This red flag is important only if we decide to delay the start of the activity past its earliest start time, ð_i, in which case we must pay attention to the start times of the activities leaving node j to avoid schedule conflicts.

Example 6.5-4

Compute the floats for the noncritical activities of the network in Example 6.5-2, and discuss their use in finalizing a schedule for the project.

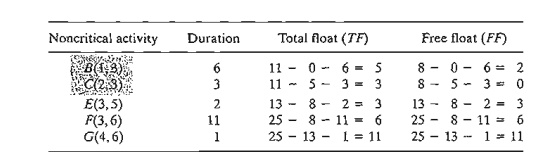
The following table summarizes the computations of the total and free floats. It is more convenient to do the calculations directly on the network using the procedure in Figure 6.42.

The computations red-flag activities Band C because their FF < TF. The remaining activities (E, F, and G) have F F = T F, and hence may be scheduled anywhere between their earliest start and latest completion times.

To investigate the significance of the red-flagged activities, consider activity B. Because its T F = 5 days, this activity can start as early as time 0 or as late as time 5 (see Figure 6.45). However, because its F F = 2 days, starting B anywhere between time 0 and time 2 will have no effect on the succeeding activities E and F. If, however, activity B must start at time 2 + d (≤ 5), then the start times of the immediately succeeding activities E and F must be pushed forward past their earliest start time (= 8) by at least d. In this manner, the precedence relationship between B and its successors E and F is preserved.

Turning to red-flagged activity C, we note that its F F = O. This means that any delay in starting C past its earliest start time (= 5) must be coupled with at least an equal delay in the start of its successor activities E and F.

TORA Moment

TORA provides useful tutorial tools for CPM calculations and for constructing the time

schedule. To  use these tools, select Project Planning => CPM Critical Path Method from Main Menu. In the output screen, you have the option to select CPM' Calculations to produce step-by-step computations of the forward pass, backward pass, and the floats or CPM Bar Chart to construct and experiment with the time schedule.

File toraEx6.5-2.txt provides TORA's data Example 6.5-2. If you elect to generate the output using the Next Step option, TORA will guide you through the details of the forward and backward pass calculations.

Figure 6.47 provides the TORA schedule produced by CPM Bar Chart option for the project of Example 6.5-2. The default bar chart automatically schedules all noncrit-ical activities as early as possible. You can study the impact of delaying the start time of a noncritical activity by using the self-explanatory drop-down lists inside the bottom left frame of the screen. The impact of a delay of a noncritical activity will be shown directly on the bar chart together with an explanation. For example, if you delay the start of activity B by more than 2 time units, the succeeding activities E and F will be

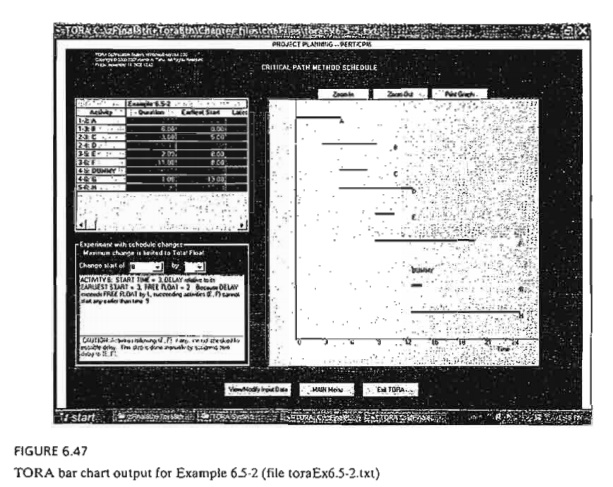
delayed by an amount equal to the difference between the delay over the free float of activity B. Specifically, given that the free float for B is 2 time units, if B is delayed by 3 time units, then E and F must be delayed by at least 3 - 2 = 1 time unit. This situation is demonstrated in Figure 6.47.

AMPLMoment

Figure 6.48 provides the AMPL model for the CPM (file amplEx6.52.txt). The model is driven by the data of Example 6.5-2. This AMPL model is a unique application because it uses indexed sets (see Section A.4) and requires no optimization. In essence, no solve command is needed, and AMPL is implemented as a pure programming language similar to Basic or C.

The nature of the computations in CPM requires representing the network by associating two indexed sets with each node: into and from. For node i, the set into [i] defines all the nodes that feed into node i, and the set from [i] defines all the nodes that are reached from node i. For example, in Example 6.5-2, from[l] = {2, 3} and into [1] is empty.

The determination of subsets from and into is achieved in the model as follows: Because D [ i , j ] can be zero when a CPM network uses dummy activities, the default value for D [ i , j] is -1 for all nonexisting arcs. Thus, the set from [ i] represents all the nodes j in the set {1 .. n} that can be reached from node i, which can happen only if D[i, j] >=0. This says that from[i] is defined by the subset {j in 1. .n:D[i, j] > =O} .

Similar reasoning applies to the determination of subsets into [i ]. The following AMPL statements automate the determination of these sets and must follow the D [i, j]  data, as shown in Figure 6.48:

Once the sets from and into have been determined, the model goes through the forward pass to compute the earliest time, ET [ i] . With the completion of this pass, we can initiate the backward pass by using

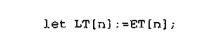
The rest of the model is needed to obtain the output shown in Figure 6.49. This output determines all the data needed to construct the CPM chart The logic of this segment is based on the computations given in Examples 6.5-2 and 6.5-4.

PROBLEM SET 6.5C

1. Given an activity (i, j) with duration D_ij and its earliest start time ð_i and its latest completion time Δ_j, determine the earliest completion and the latest start times of (i,j).

2. What are the total and free floats of a critical activity? Explain.

*3. For each of the following activities, determine the maximum delay in the starting time rel-ative to its earliest start time that will allow all the immediately succeeding activities to be scheduled anywhere between their earliest and latest completion times.

                                                                                                             i.      T F = 10, FF =  10, D =  4

                                                                                                           ii.      TF = 10,FF = S,D = 4

                                                                                                        iii.      TF =  1O,FF = O,D = 4

4. In Example 6.5-4, use the floats to answer the following:

a.     If activity B is started at time 1, and activity C is started at time 5, determine the earliest start times for E and F.

b.     If activity B is started at time 3, and activity C is started at time 7, determine the earliest start times for E and F.

c.      How is the scheduling of other activities impacted if activity B starts at time 6?

*5. In the project of Example 6.5-2 (Figure 6.42), assume that the durations of activities B and F are changed from 6 and 11 days to 20 and 25 days, respectively.

a.     Determine the critical path.

b.     Determine the total and free floats for the network, and identify the red-flagged activities.

c.     If activity A is started at time 5, determine the earliest possible start times for activi-ties C, D, E,and G.

d.     If activities F, G, and H require the same equipment, determine the minimum num-ber of units needed of this equipment.

6. Compute the floats and identify the red-flagged activities for the projects (a) and (b) in Figure 6.44, then develop the time schedules under the following conditions:

Project (a)

                                                                                           i.      Activity (1,5) cannot start any earlier than time 14.

                                                            ii.    Activities (5,6) and (5,7) use the same equipment, of which only one unit is available.

                                                                                      iii.      All other activities start as early as possible.

Project (b)

                                                                   i.      Activity (1,3) must be scheduled at its earliest start time while accounting for the requirement that (1,2), (1, 3), and (1,6) use a special piece of equipment, of which 1 unit only is available.

                                                                 ii.      All other activities start as early as possible.