Chapter: Operations Research: An Introduction : Network Models
CPM AND PERT: linear Programming Formulation of CPM
linear Programming Formulation of CPM
A CPM
problem can thought of as the opposite of the shortest-route problem (Section
6.3), in the sense that we are interested in finding the Longest route of a unit flow entering at the start node and
terminating at the finish node. We can thus apply the shortest route LP
formulation in Section 6.3.3 to CPM in the following manner. Define
xij = Amount of flow in activity (i, j), for all defined i and j
Dij = Duration of activity (i, j), for all
defined i and j
Thus, the
objective function of the linear program becomes
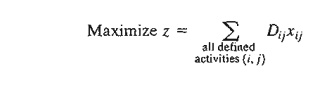
(Compare
with the shortest route LP formulation in Section 6.3.3 where the objective
function is minimized.) For each node, there is one constraint that represents
the conservation of flow:
Total
input flow = Total output flow
All the
variables, Xij, are
nonnegative.
Example
6.5-5
The· LP
formulation of the project of Example 6.5-2 (Figure 6.42 ) is given below. Note
that nodes 1 and 6 are the start and finish nodes, respectively.

The solution
defines the critical path as A --> D -->
Dummy ---> H, and the duration of the project
is 25 days. The LP solution is not complete, because it determines the critical
path, but does not provide the data needed to construct the CPM chart. We have seen
in Figure 6.48, however, that AMPL can be used to provide all the needed
information without the LP optimization.
PROBLEM
SET 6.5D
1. Use LP
to determine the critical path for the project network in Figure 6.43.
2. Use LP
to determine the critical path for the project networks in Figure 6.44.
Related Topics