Examples of the Shortest-Route Applications or Problem

SHORTEST-ROUTE PROBLEM

The shortest-route problem determines the shortest route between a source and destination in a transportation network. Other situations can be represented by the same model, as illustrated by the following examples.

Examples of the Shortest-Route Applications

Example 6.3-1 (Equipment Replacement)

RentCar is developing a replacement policy for its car fleet for a 4-year planning horizon. At the start of each year, a decision is made as to whether a car should be kept in operation or replaced.

A car must be in service a minimum of 1 year and a maximum of 3 years. TIle following table provides the replacement cost as a function of the year a car is acquired and the number of years in operation.

TIle problem can be formulated as a network in which nodes 1 to 5 represent the start of years 1 to 5. Arcs from nodel (year 1) can reach only nodes 2,3, and 4 because a car must be in operation between 1 and 3 years. The arcs from the other nodes can be interpreted similarly. The length of each arc equals the replacement cost. The solution of the problem is equivalent to find-ing the shortest route between nodes 1 and 5.

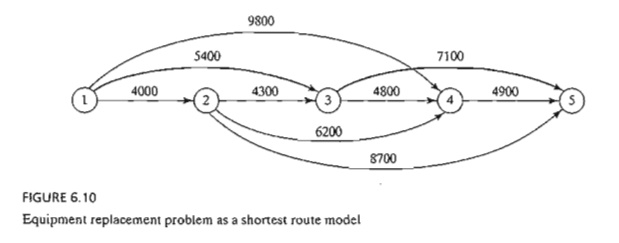
Figure 6.10 shows the resulting network. Using TORA, the shortest route (shown by the thick path) is 1 -> 3 -> 5. The solution means that a car acquired at the start of year 1 (node 1) must be replaced after 2 years at the start of year 3 (node 3). The replacement car will then be kept in service until the end of year 4. The total cost of this replacement policy is $12,500 (= $5400 + $7100).

Example 6.3-2    (Most Reliable Route)

1. Q. Smart drives daily to work. Having just completed a course in network analysis, Smart is able to determine the shortest route to work. Unfortunately, the selected route is heavily patrolled by police, and with all the fines paid for speeding, the shortest route may not be the best choice. Smart has thus decided to choose a route that maximizes the probability of not being stopped by police.

The network in Figure 6.11 shows the possible routes between home and work, and the associated probabilities of not being stopped on each segment. The probability of not being

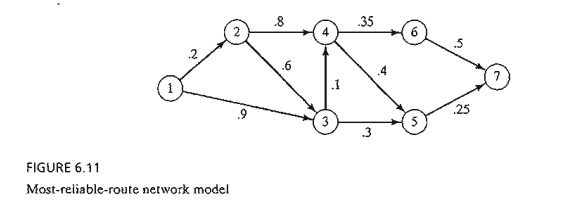
stopped on a route is the product of the probabilities associated with its segments. For example, the probability of not receiving a fine on the route 1 -> 3 -> 5 -> 7 is .9 X .3 X .25 = .0675. Smart's objective is to select the route that maximizes the probability of not being fined.

The problem can be formulated as a shortest-route model by using a logarithmic transformation that converts the product probability into the sum of the logarithms of probabilities that is, if p_lk = p₁ X p₂ X ... X p_k is the probability of not being stopped, then log p_lk = log p₁ + log p₂ + ... + log p_k.

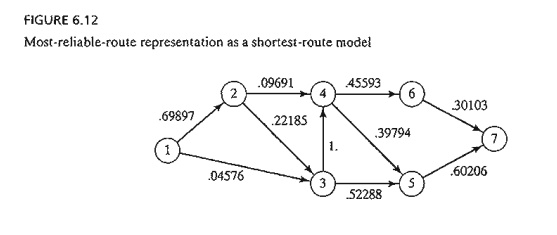
Mathematically, the maximization of log p_lk is equivalent to the maximization of log p_1k. Because log p_1k  ≤ 0, the maximization of log p_1k is equivalent to the minimization of -log p_1k. Using this transformation, the individual probabilities pj in Figure 6.11 are replaced with -log p_i for all j in the network, thus yielding the shortest-route network in Figure 6.12.

Using TORA, the shortest route in Figure 6.12 is defined by the nodes 1,3,5, and 7 with a corresponding "length" of 1.1707 (= -log P₁₇). Thus, the maximum probability of not being stopped is p₁₇ = .0675 only, not very encouraging news for Smart!

Example 6.3-3    (Three-Jug Puzzle)

An 8-gallon jug is filled with fluid. Given two empty 5- and 3-gallon jugs, we want to divide the 8 gallons of fluid into two equal parts using the three jugs. No other measuring devices are allowed. What is the smallest number of transfers (decantations) needed to achieve this result?

You probably can guess the solution to this puzzle. Nevertheless, the solution process can be systematized by representing the problem as a shortest-route problem.

A node is defined to represent the amount of fluid in the 8-,5-, and 3-gallon jugs, respec-tively. This means that the network starts with node (8, 0, 0) and terminates with the desired

solution node (4,4,0). A new node is generated from the current node by decanting fluid from one jug into another.

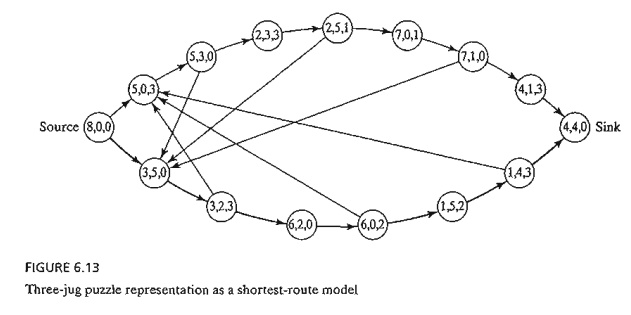
Figure 6.13 shows different routes that lead from the start node (8,0,0) to the end node (4, 4, 0). The arc between two successive nodes represents a single transfer, and hence can be assumed to have a length of 1 unit. The problem thus reduces to determining the shortest route between node (8,0,0) and node (4,4,0).

The optimal solution, given by the bottom path in Figure 6.13, requires 7 transfers.

PROBLEM SET 6.3A

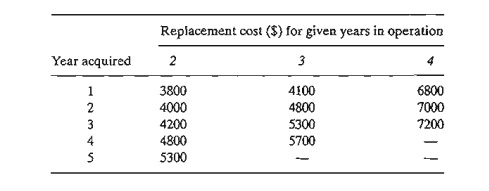
*1. Reconstruct the equipment replacement model of Example 6.3-1, assuming that a car must be kept in service at least 2 years, with a maximum service life of 4 years. The planning horizon is from the start of year 1 to the end of year 5. The following table provides the necessary data.

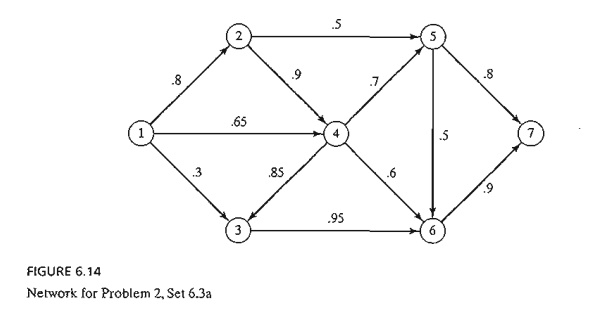
2. Figure 6.14 provides the communication network between two stations, 1 and 7. The probability that a link in the network will operate without failure is shown on each arc. Messages are sent from station 1 to station 7, and the objective is to determine the route.

 that will maximize the probability of a successful transmission. Formulate the situation as a shortest-route model and determine the optimum solution.

3. Production Planning. Directeo sells an item whose demands over the next 4 months are 100,140,210, and 180 units, respectively. The company can stock just enough supply to meet each month's demand, or it can overstock to meet the demand for two or more successive and consecutive months. In the latter case, a holding cost of $1.20 is charged per overstocked unit per month. Directeo estimates the unit purchase prices for the next 4 months to be $15, $12, $10, and $14, respectively. A selup cost of $200 is incurred each time a purchase order is placed. The company wants to develop a purchasing plan that will minimize the total costs of ordering, purchasing, and holding the item in stock. Formulate the problem as a shortest-route model, and use TORA to find the optimum solution.

*4. Knapsack Problem. A hiker has a 5-ft³ backpack and needs to decide on the most valuable items to take on the hiking trip. There are three items from which to choose. Their volumes are 2, 3, and 4 ft3, and the hiker estimates their associated values on a scale from oto 100 as 30,50, and 70, respectively. Express the problem as longest-route network, and find the optimal solution. (Hint: A node in the network may be defined as [i, v], where i is the item number considered for packing, and v is the volume remaining immediately before a decision is made on i.)

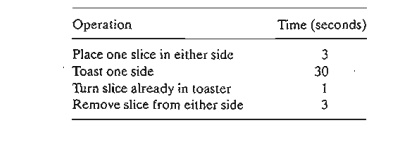
5. An old-fashioned electric toaster has two spring-loaded base-hinged doors. The two doors open outward in opposite directions away from the heating element. A slice of bread is toasted one side at a time by pushing open one of the doors with one hand and placing the slice with the other hand. After one side is toasted, the slice is turned over to get the other side toasted. The goal is to determine the sequence of operations (placing, toasting, turning, and removing) needed to toast three slices of bread in the shortest possible time. Formulate the problem as a shortest-route model, using the following elemental times for the different operations: