CPM AND PERT: Critical Path (CPM) Computations

Critical Path (CPM) Computations

The end result in CPM is the construction of the time schedule for the project (see Figure 6.38). To achieve this objective conveniently, we carry out special computations that produce the following information:

a.     Total duration needed to complete the project.

b.     Classification of the activities of the project as critical and noncritical.

An activity is said to be critical if there is no "leeway" in determining its start and finish times. A noncritical activity allows some scheduling slack, so that the start time of the activity can be advanced or delayed within limits without affecting the comple-tion date of the entire project.

To carry out the necessary computations, we define an event as a point in time at which activities are terminated and others are started. In terms of the network, an event corresponds to a node. Define

The definitions of the earliest and latest occurrences of event j are specified relative to the start and completion dates of the entire project.

The critical path calculations involve two passes: The forward pass detennines the earliest occurrence times of the events, and the backward pass calculates their latest occurrence times.

Forward Pass (Earliest Occurrence limes, ð). The computations start at node 1 and advance recursively to end node n.

Initial Step. Set ð ₁ =  0 to indicate that the project starts at time O.

General Step j. Given that nodes p, q,…. , and v are linked directly to node j by incoming activities (p, j), (q, j), , and (v, j) and that the earliest occurrence times of events (nodes) p, q, ... , and v have already been computed, then the earliest occurrence time of event j is computed as

The three conditions state that the earliest and latest occurrence times of end nodes i and j are equal and the duration D_ij fits "tightly" in the specified time span. An activity that does not satisfy all three conditions is thus noncritical.

By definition, the critical activities of a network must constitute an uninterrupted path that spans the entire network from start to finish.

Example 6.5-2

Determine the critical path for the project network in Figure 6.42 . All the durations are in days.

Forward Pass

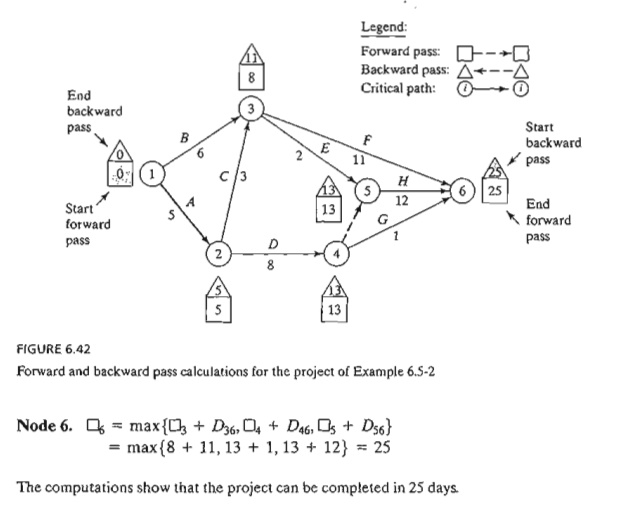
The forward and backward pass computations can be made directly on the network as shown in Figure 6.42. Applying the rules for determining the critical activities, the critical path is 1 -> 2 -> 4 -> 5 -> 6, which, as should be expected, spans the network from start (node 1) to finish (node 6). The sum of the durations of the critical activities [(1,2), (2, 4), (4, 5), and (5, 6)J equals the duration of the project (= 25 days). Observe that activity (4,6) satisfies the first two conditions for a critical activity

Hence, the activity is noncritical.

PROBLEM SET 6.5B

*1.  Determine the critical path for the project network in Figure 6.43.

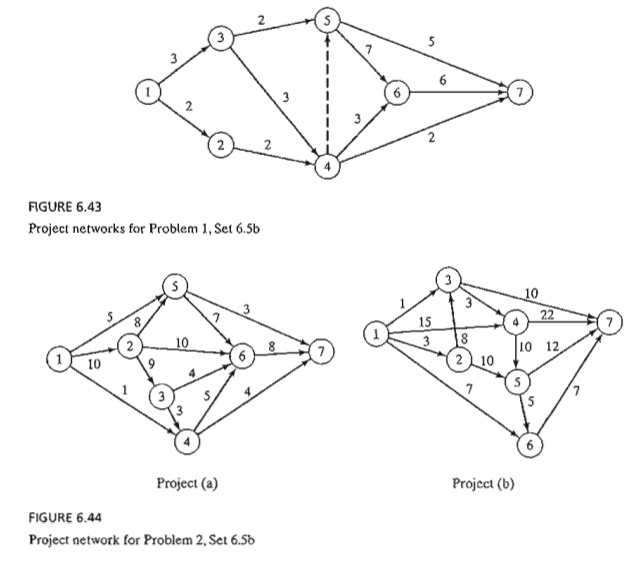
2. Determine the critical path for the project networks in Figure 6.44.

3. Determine the critical path for the project in Problem 6, Set6.5a.

4. Determine the critical path for the project in Problem 8, Set 6.5a.

5. Determine the critical path for the project in Problem 9, Set 6.5a.

6. Determine the critical path for the project in Problem 10, Set 6.5a.