Chapter: Genetics and Molecular Biology: DNA Synthesis
How Fast Could DNA Be Replicated? - Physiological Aspects
How Fast Could DNA Be Replicated?
In the preceding sections we have seen that the
bacterial chromosome is replicated by two synthesis forks moving away from a
replication origin at a chain elongation speed of about 500 nucleotides per
second for cells growing at 37°. How does this rate compare to the maximum rate
at which nucleotides could diffuse to the DNA polymerase? This question is one
specific example of a general concern about intracellular conditions. Often it
is important to know an approximate time required for a particular molecule to
diffuse to a site.
Consider a polymerase molecule to be sitting in a
sea of infinite dimensions containing the substrate. Even though the polymerase
moves along the DNA as it synthesizes, we will consider it to be at rest since
the processes of diffusion of the nucleotides which we are consid-ering here
are much faster. We will consider that the elongation rate of the enzyme is
limited by the diffusion of nucleotides to its active site. Under these
conditions, the concentration of substrate is zero on the surface of a sphere
of radius r0
constituting the active site of the enzyme (Fig. 3.21). Any substrate molecules
crossing the surface into this region disappear. At great distances from the
enzyme, the concentration of substrate remains unaltered. These represent the
boundary conditions of the situation, which requires a mathematical formulation
to deter-mine the concentrations at intermediate positions.
The basic diffusion equation relates time and
position changes in the concentration C
of a diffusible quantity. As diffusion to an enzyme can be considered to be
spherically symmetric, the diffusion equation can be written and solved in
spherical coordinates involving only the radius r, the concentration C,
the diffusion coefficient D, and time t:

Figure
3.21 A DNA polymerase possessing an
active site of radiusr0into
whichnucleotides disappear as fast as they can reach the enzyme and the
expected nucleotide concentration as a function of distance from the enzyme.

The solution to this equation, which satisfies the
conditions of being constant at large r
and zero at r = r0, is
![]()
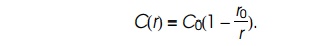
The flow rate J
of substrate to the enzyme can now be calculated from the equation, giving the
flux J:
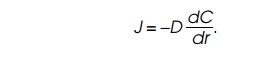
The total flow through a sphere centered on the
enzyme yields
Flow
= 4πr2J
= 4πDr0C0.
The final
result shows that the flow is independent of the size of the sphere chosen for
the calculation. This is as it should be. The only place where material is
being destroyed is at the active site of the enzyme. Everywhere else, matter
must be conserved. In steady state there is no change of the concentration of
substrate at any position, and hence the net amount flowing through the surface
of all spheres must be equal.
To
calculate the flow rate of nucleoside triphosphates to the DNA polymerase, we
must insert numerical values in the final result. The concentration of
deoxynucleoside triphosphates in cells is between 1 mM and 0.1 mM. We will use
0.1 mM, which is 10- 4 moles per liter or 10-7 moles per
cm3. Taking the diffusion constant to be 10-7 cm2/sec
and r0to be 10Å, we find
that the flow is 10-20moles/sec or about 6,000molecules/sec. The
rate of DNA synthesis per enzyme molecule of about 500 nucleoside triphosphates
per second is less than 10% of the upper limit on the elongation rate set by
the laws of diffusion. Considering that the actual active site for certain
capture of the triphosphate might be much smaller than 10 Å, the elongation
rate of DNA seems remarkably high.
Related Topics