Chapter: Medical Physiology: The Microcirculation and the Lymphatic System: Capillary Fluid Exchange, Interstitial Fluid, and Lymph Flow
Fluid Filtration Across Capillaries Is Determined by Hydrostatic and Colloid Osmotic Pressures, and Capillary Filtration Coefficient
Fluid Filtration Across Capillaries Is Determined by Hydrostatic and Colloid Osmotic Pressures, and Capillary Filtration Coefficient
The hydrostatic pressure in the capillaries tends to force fluid and its dissolved substances through the capillary pores into the interstitial spaces. Conversely, osmotic pressure caused by the plasma proteins (called colloid osmotic pressure) tends to cause fluid movement by osmosis from the interstitial spaces into the blood. This osmotic pressure exerted by the plasma proteins normally prevents significant loss of fluid volume from the blood into the interstitial spaces.
Also important is the lymphatic system, which returns to the circulation the small amounts of excess protein and fluid that leak from the blood into the interstitial spaces. In the remainder, we discuss the mechanisms that control capillary filtration and lymph flow function together to regulate the respective volumes of the plasma and the interstitial fluid.
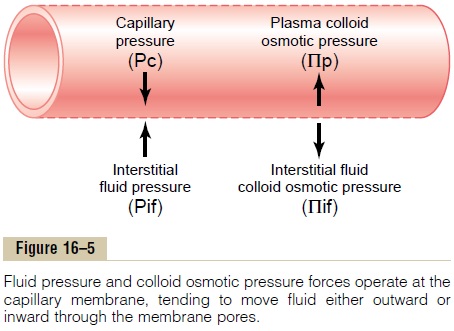
Four Primary Hydrostatic and Colloid Osmotic Forces Determine Fluid Movement Through the Capillary Membrane. Figure16–5 shows the four primary forces that determine whether fluid will move out of the blood into the inter-stitial fluid or in the opposite direction. These forces, called “Starling forces” in honor of the physiologist who first demonstrated their importance, are:
1. The capillary pressure (Pc), which tends to force fluid outward through the capillary membrane.
2. The interstitial fluid pressure (Pif), which tends to force fluid inward through the capillary membrane when Pif is positive but outward when Pif is negative.
3. The capillary plasma colloid osmotic pressure (Pp), which tends to cause osmosis of fluid inward through the capillary membrane.
4. The interstitial fluid colloid osmotic pressure (Pif), which tends to cause osmosis of fluid outward through the capillary membrane.
If the sum of these forces, the net filtration pressure, is positive, there will be a net fluid filtration across the capillaries. If the sum of the Starling forces is negative, there will be a net fluid absorption from the intersti-tial spaces into the capillaries. The net filtration pres-sure (NFP) is calculated as:
NFP = Pc - Pif - Πp + Πif
As discussed later, the NFP is slightly positive under normal conditions, resulting in a net filtration of fluid across the capillaries into the interstitial space in most organs. The rate of fluid filtration in a tissue is also determined by the number and size of the pores in each capillary as well as the number of capillaries in which blood is flowing. These factors are usually expressed together as thecapillary filtration coefficient (Kf). The Kf is therefore a measure of the capacity of the capillary membranes to filter water for a given NFP and is usually expressed as ml/min per mm Hg net filtration pressure.
The rate of capillary fluid filtration is therefore determined as:
Filtration = Kf x NFP
In the following sections we discuss in detail each of the forces that determine the rate of capillary fluid filtration.
Capillary Hydrostatic Pressure
Two experimental methods have been used to esti-mate the capillary hydrostatic pressure: (1) directmicropipette cannulation of the capillaries, which hasgiven an average mean capillary pressure of about 25 mm Hg, and (2) indirect functional measurement of thecapillary pressure, which has given a capillary pressureaveraging about 17 mm Hg.
Micropipette Method for Measuring Capillary Pressure. Tomeasure pressure in a capillary by cannulation, a microscopic glass pipette is thrust directly into the cap-illary, and the pressure is measured by an appropriate micromanometer system. Using this method, capillary pressures have been measured in capillaries of exposed tissues of animals and in large capillary loops of the eponychium at the base of the fingernail in humans. These measurements have given pressures of 30 to 40 mm Hg in the arterial ends of the capillaries, 10 to 15 mm Hg in the venous ends, and about 25 mm Hg in the middle.
Isogravimetric Method for Indirectly Measuring “Functional” Capillary Pressure. Figure 16–6 demonstrates aniso-gravimetric method for indirectly estimating capillarypressure. This figure shows a section of gut held up by one arm of a gravimetric balance. Blood is perfused through the blood vessels of the gut wall. When the arterial pressure is decreased, the resulting decrease in capillary pressure allows the osmotic pressure of the plasma proteins to cause absorption of fluid out of the gut wall and makes the weight of the gut decrease. This immediately causes displacement of the balance arm. To prevent this weight decrease, the venous pressure is increased an amount sufficient to overcome the effect of decreasing the arterial pressure. In other words, the capillary pressure is kept constant while simultaneously (1) decreasing the arterial pressure and (2) increasing the venous pressure.
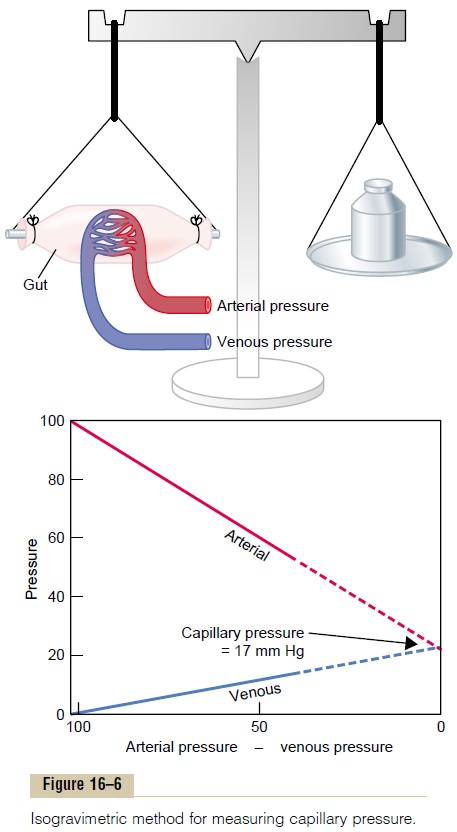
In the graph in the lower part of the figure, the changes in arterial and venous pressures that exactly nullify all weight changes are shown. The arterial and venous lines meet each other at a value of 17 mm Hg. Therefore, the capillary pressure must have remained at this same level of 17 mm Hg throughout these maneuvers; otherwise, either filtration or absorption of
Thus, in a roundabout way, the “functional” capillary pressure is measured to be about 17 mm Hg.
Why Is the Functional Capillary Pressure Lower than Capillary Pressure Measured by the Micropipette Method? It is clearthat the aforementioned two methods do not give the same capillary pressure. However, the isogravimetric method determines the capillary pressure that exactly balances all the forces tending to move fluid into or out of the capillaries. Because such a balance of forces is the normal state, the average functional capillary pressure must be close to the pressure measured by the isogravimetric method. Therefore, one is justified in believing that the true functional capillary pressure averages about 17 mm Hg.
It is easy to explain why the cannulation methods give higher pressure values. The most important reason is that these measurements usually are made in capillaries whose arterial ends are open and when blood is actively flowing into the capillary. However, it should be recalled from the earlier discussion of cap-illary vasomotion that the metarterioles and precapil-lary sphincters normally are closed during a large part of the vasomotion cycle. When closed, the pressure in the capillaries beyond the closures should be almost equal to the pressure at the venous ends of the capil-laries, about 10 mm Hg. Therefore, when averaged over a period of time, one would expect the functional mean capillary pressure to be much nearer to the pres-sure in the venous ends of the capillaries than to the pressure in the arterial ends.
There are two other reasons why the functional cap-illary pressure is less than the values measured by can-nulation. First, there are far more capillaries nearer to the venules than to the arterioles. Second, the venous capillaries are several times as permeable as the arte-rial capillaries. Both of these effects further decrease the functional capillary pressure to a lower value.
Interstitial Fluid Hydrostatic Pressure
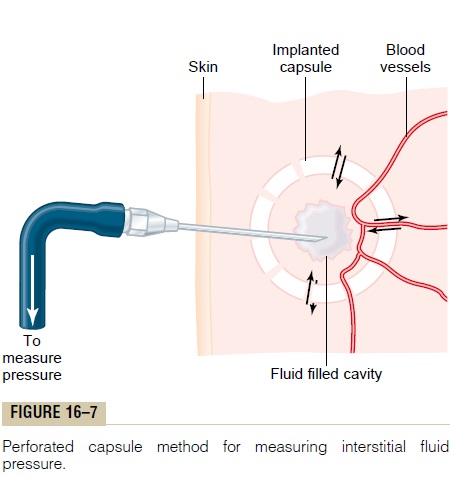
As is true for the measurement of capillary pressure, there are several methods for measuring interstitial fluid pressure, and each of these gives slightly differ-ent values but usually values that are a few millime-ters of mercury less than atmospheric pressure, that is, values called negative interstitial fluid pressure. The methods most widely used have been (1) direct can-nulation of the tissues with a micropipette, (2) meas-urement of the pressure from implanted perforated capsules, and (3) measurement of the pressure from a cotton wick inserted into the tissue.
Measurement of Interstitial Fluid Pressure Using the Micropipette. The same type of micropipette used formeasuring capillary pressure can also be used in some tissues for measuring interstitial fluid pressure. The tip of the micropipette is about 1 micrometer in diameter, but even this is 20 or more times larger than the sizes of the spaces between the proteoglycan filaments of the interstitium. Therefore, the pressure that is measured is probably the pressure in a free fluid pocket.
The first pressures measured using the micropipette method ranged from -1 to +2 mm Hg but were usually slightly positive. With experience and improved equip-ment for making such measurements, more recent pres-sures have averaged about -2 mm Hg, giving average pressure values in loose tissues, such as skin, that are slightly less than atmospheric pressure.
Measurement of Interstitial Free Fluid Pressure in Implanted Per- forated Hollow Capsules. Interstitial freefluid pressuremeasured by this method when using 2-centimeter diameter capsules in normal loose subcutaneous tissue averages about -6 mm Hg, but with smaller capsules, the values are not greatly different from the -2 mm Hg measured by the micropipette in Figure 16-7.
Measurement of Interstitial Free Fluid Pressure by Means of a Cotton Wick. Still another method is to insert into atissue a small Teflon tube with about eight cotton fibers protruding from its end. The cotton fibers form a “wick” that makes excellent contact with the tissue fluids and transmits interstitial fluid pressure into the Teflon tube: the pressure can then be measured from the tube by usual manometric means. Pressures measured by this technique in loose subcutaneous tissue also have been negative, usually measuring -1 to -3 mm Hg.
Interstitial Fluid Pressures in Tightly Encased Tissues
Some tissues of the body are surrounded by tight encasements, such as the cranial vault around the brain, the strong fibrous capsule around the kidney, the fibrous sheaths around the muscles, and the sclera around the eye. In most of these, regardless of the method used for measurement, the interstitial fluid pressures are usually positive. However, these intersti-tial fluid pressures almost invariably are still less than the pressures exerted on the outsides of the tissues by their encasements. For instance, the cerebrospinal fluid pressure surrounding the brain of an animal lying on its side averages about +10 mm Hg, whereas the braininterstitial fluid pressureaverages about+4 to+6 mmHg. In the kidneys, the capsular pressure surrounding the kidney averages about +13 mm Hg, whereas the reported renal interstitial fluid pressures have averaged about +6 mm Hg. Thus, if one remembers that the pressure exerted on the skin is atmospheric pressure, which is considered to be zero pressure, one might for-mulate a general rule that the normal interstitial fluid pressure is usually several millimeters of mercury neg-ative with respect to the pressure that surrounds each tissue.
Is the True Interstitial Fluid Pressure in Loose Subcutaneous Tissue Subatmospheric?
The concept that the interstitial fluid pressure is sub-atmospheric in many if not most tissues of the body began with clinical observations that could not be explained by the previously held concept that intersti-tial fluid pressure was always positive. Some of the per-tinent observations are the following:
1. When a skin graft is placed on a concave surface of the body, such as in an eye socket after removal of the eye, before the skin becomes attached to the sublying socket, fluid tends to collect underneath the graft. Also, the skin attempts to shorten, with the result that it tends to pull it away from the concavity. Nevertheless, some negative force underneath the skin causes absorption of the fluid and usually literally pulls the skin back into the concavity.
2.Less than 1 mm Hg of positive pressure is required to inject tremendous volumes of fluid into loose subcutaneous tissues, such as beneath the lower eyelid, in the axillary space, and in the scrotum. Amounts of fluid calculated to be more than 100 times the amount of fluid normally in the interstitial space, when injected into these areas, cause no more than about 2 mm Hg of positive pressure. The importance of these observations is that they show that such tissues do not have strong fibers that can prevent the accumulation of fluid. Therefore, some other mechanism, such as a negative fluid pressure system, must be available to prevent such fluid accumulation.
3.In most natural cavities of the body where there is free fluid in dynamic equilibrium with the surrounding interstitial fluids, the pressures that have been measured have been negative. Some of these are the following:
Intrapleural space: -8 mm Hg
Joint synovial spaces: -4 to -6 mm Hg
Epidural space: -4 to -6 mm Hg
4.The implanted capsule for measuring the interstitial fluid pressure can be used to record dynamic changes in this pressure. The changes are approximately those that one would calculate to occur (1) when the arterial pressure is increased or decreased, (2) when fluid is injected into the surrounding tissue space, or (3) when a highly concentrated colloid osmotic agent is injected into the blood to absorb fluid from the tissue spaces. It is not likely that these dynamic changes could be recorded this accurately unless the capsule pressure closely approximated the true interstitial pressure.
Summary—An Average Value for Negative Interstitial Fluid Pressure in Loose Subcutaneous Tissue. Although theaforementioned different methods give slightly differ-ent values for interstitial fluid pressure, there currently is a general belief among most physiologists that the true interstitial fluid pressure in loose subcutaneous tissue is slightly less subatmospheric, averaging about -3 mm Hg.
Pumping by the Lymphatic System Is the Basic Cause of the Negative Interstitial Fluid Pressure
The lymphatic system is discussed, but we need to understand here the basic role that this system plays in determining interstitial fluid pressure. The lymphatic system is a “scavenger” system that removes excess fluid, excess protein molecules, debris, and other matter from the tissue spaces. Normally, when fluid enters the terminal lymphatic capillaries, the lymph vessel walls automatically contract for a few seconds and pump the fluid into the blood circulation. This overall process creates the slight negative pres-sure that has been measured for fluid in the interstitial spaces.
Plasma Colloid Osmotic Pressure
Proteins in the Plasma Cause Colloid Osmotic Pressure. In the basic discussion of osmotic pressure, it was pointed out that only those molecules or ions that fail to pass through the pores of a semiperme-able membrane exert osmotic pressure. Because the proteins are the only dissolved constituents in the plasma and interstitial fluids that do not readily pass through the capillary pores, it is the proteins of the plasma and interstitial fluids that are responsible for the osmotic pressures on the two sides of the capillary membrane. To distinguish this osmotic pressure from that which occurs at the cell membrane, it is called either colloid osmotic pressure oroncotic pressure. The term “colloid” osmotic pressure is derived from the fact that a protein solution resembles a colloidal solu-tion despite the fact that it is actually a true molecu-lar solution.
Normal Values for Plasma Colloid Osmotic Pressure. Thecolloid osmotic pressure of normal human plasma averages about 28 mm Hg; 19 mm of this is caused by molecular effects of the dissolved protein and 9 mm by the Donnan effect—that is, extra osmotic pressure caused by sodium, potassium, and the other cations held in the plasma by the proteins
Effect of the Different Plasma Proteins on Colloid Osmotic Pressure. The plasma proteins are a mixture that con-tains albumin, with an average molecular weight of 69,000; globulins, 140,000; and fibrinogen, 400,000. Thus, 1 gram of globulin contains only half as many molecules as 1 gram of albumin, and 1 gram of fibrinogen contains only one sixth as many molecules as 1 gram of albumin. It should be recalled from the discussion of osmotic pressure that osmotic pressure is determined by the number of moleculesdissolved in a fluid rather than by the mass of these molecules. Therefore, when corrected for number of molecules rather than mass, the following chart gives both the relative mass concentrations (g/dl) of the different types of proteins in normal plasma and their respective contributions to the total plasma colloid osmotic pressure (Πp).
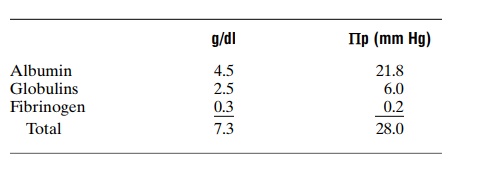
Thus, about 80 per cent of the total colloid osmotic pressure of the plasma results from the albumin frac-tion, 20 per cent from the globulins, and almost none from the fibrinogen. Therefore, from the point of view of capillary and tissue fluid dynamics, it is mainly albumin that is important.
Interstitial Fluid Colloid Osmotic Pressure
Although the size of the usual capillary pore is smaller than the molecular sizes of the plasma proteins, this is not true of all the pores. Therefore, small amounts of plasma proteins do leak through the pores into the interstitial spaces.
The total quantity of protein in the entire 12 liters of interstitial fluid of the body is slightly greater than the total quantity of protein in the plasma itself, but because this volume is four times the volume of plasma, the average protein concentration of the inter- stitial fluid is usually only 40 per cent of that in plasma, or about 3 g/dl. Quantitatively, one finds that the average interstitial fluid colloid osmotic pressure for this concentration of proteins is about 8 mm Hg.
Exchange of Fluid Volume Through the Capillary Membrane
Now that the different factors affecting fluid move- ment through the capillary membrane have been discussed, it is possible to put all these together to see how the capillary system maintains normal fluid volume distribution between the plasma and the inter- stitial fluid.
The average capillary pressure at the arterial ends of the capillaries is 15 to 25 mm Hg greater than at the venous ends. Because of this difference, fluid “filters” out of the capillaries at their arterial ends, but at their venous ends fluid is reabsorbed back into the capillar- ies. Thus, a small amount of fluid actually “flows” through the tissues from the arterial ends of the capillaries to the venous ends. The dynamics of this flow are as follows.
Analysis of the Forces Causing Filtration at the Arterial End of the Capillary. The approximate average forces operative at the arterial end of the capillary that cause movement through the capillary membrane are shown as follows:

Thus, the summation of forces at the arterial end of the capillary shows a net filtration pressure of 13 mm Hg, tending to move fluid outward through the capil-lary pores.
This 13 mm Hg filtration pressure causes, on the average, about 1/200 of the plasma in the flowing blood to filter out of the arterial ends of the capillaries into the interstitial spaces each time the blood passes through the capillaries.
Analysis of Reabsorption at the Venous End of the Capillary.
The low blood pressure at the venous end of the capillary changes the balance of forces in favor of absorp-tion as follows:

Thus, the force that causes fluid to move into the capillary, 28 mm Hg, is greater than that opposing reabsorption, 21 mm Hg. The difference, 7 mm Hg, is the net reabsorption pressure at the venous ends of the capillaries. This reabsorption pressure is considerably less than the filtration pressure at the capillary arterial ends, but remember that the venous capillaries are more numerous and more permeable than the arterial capillaries, so that less reabsorption pressure is required to cause inward movement of fluid.
The reabsorption pressure causes about nine tenths of the fluid that has filtered out of the arterial ends of the capillaries to be reabsorbed at the venous ends.
The remaining one tenth flows into the lymph vessels and returns to the circulating blood.
Starling Equilibrium for Capillary Exchange
E. H. Starling pointed out over a century ago that under normal conditions, a state of near-equilibrium exists at the capillary membrane. That is, the amount of fluid filtering outward from the arterial ends of cap-illaries equals almost exactly the fluid returned to the circulation by absorption. The slight disequilibrium that does occur accounts for the small amount of fluid that is eventually returned by way of the lymphatics.
The following chart shows the principles of the Star-ling equilibrium. For this chart, the pressures in the arte-rial and venous capillaries are averaged to calculate mean functional capillary pressure for the entire length of the capillary. This calculates to be 17.3 mm Hg.

Thus, for the total capillary circulation, we find a near-equilibrium between the total outward forces, 28.3 mm Hg, and the total inward force, 28.0 mm Hg. This slight imbalance of forces, 0.3 mm Hg, causes slightly more filtration of fluid into the interstitial spaces than reabsorption. This slight excess of filtration is called net filtration, and it is the fluid that must be returned to the circulation through the lymphatics. The normal rate of net filtration in the entire body is only about 2 milliliters per minute.
Filtration Coefficient. In the above example, an averagenet imbalance of forces at the capillary membranes of 0.3 mm Hg causes net fluid filtration in the entire body of 2 ml/min. Expressing this for each millimeter of mercury imbalance, one finds a net filtration rate of 6.67 milliliters of fluid per minute per millimeter of mercury for the entire body. This is called the whole body capillary filtration coefficient.
The filtration coefficient can also be expressed for separate parts of the body in terms of rate of filtration per minute per millimeter of mercury per 100 grams of tissue. On this basis, the filtration coefficient of the average tissue is about 0.01 ml/min/mm Hg/100 g of tissue. But, because of extreme differences in perme-abilities of the capillary systems in different tissues, this coefficient varies more than 100-fold among the different tissues. It is very small in both brain and muscle, moderately large in subcutaneous tissue, large in the intestine, and extreme in the liver and glomeru-lus of the kidney where the pores are either numerous or wide open. By the same token, the permeation of proteins through the capillary membranes varies greatly as well. The concentration of protein in the interstitial fluid of muscles is about 1.5 g/dl; in subcu-taneous tissue, 2 g/dl; in intestine, 4 g/dl; and in liver, 6 g/dl.
Effect of Abnormal Imbalance of Forces at the Capillary Membrane
If the mean capillary pressure rises above 17 mm Hg, the net force tending to cause filtration of fluid into the tissue spaces rises. Thus, a 20 mm Hg rise in mean cap-illary pressure causes an increase in net filtration pres-sure from 0.3 mm Hg to 20.3 mm Hg, which results in 68 times as much net filtration of fluid into the inter-stitial spaces as normally occurs. To prevent accumu-lation of excess fluid in these spaces would require 68 times the normal flow of fluid into the lymphatic system, an amount that is 2 to 5 times too much for the lymphatics to carry away. As a result, fluid will begin to accumulate in the interstitial spaces, and edema will result.
Conversely, if the capillary pressure falls very low, net reabsorption of fluid into the capillaries will occur instead of net filtration, and the blood volume will increase at the expense of the interstitial fluid volume.
Related Topics