Physics - Electromagnetic Waves: Exercises and Example Solved Numerical problems | 12th Physics : Electromagnetic Waves
Chapter: 12th Physics : Electromagnetic Waves
Electromagnetic Waves: Exercises and Example Solved Numerical problems
Numerical problems
1. Consider a parallel plate capacitor whose plates are closely spaced. Let R be the radius of the plates and the current in the wire connected to the plates is 5 A, calculate the displacement current through the surface passing between the plates by directly calculating the rate of change of flux of electric field through the surface.
Answer: Id = Ic = 5 A
2. A transmitter consists of LC circuit with an inductance of 1 µH and a capacitance of 1 µF. What is the wavelength of the electromagnetic waves it emits?
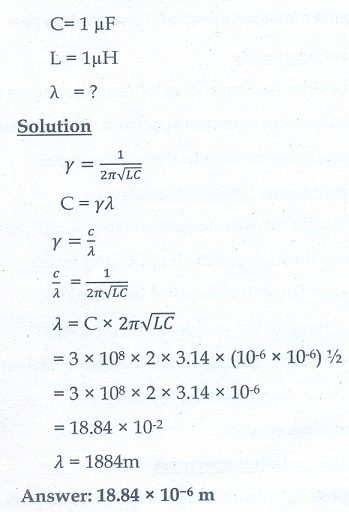
Answer: 18.84 × 10−6 m
3. A pulse of light of duration 10−6 s is absorbed completely by a small object initially at rest. If the power of the pulse is 60 × 10−3 W, calculate the final momentum of the object.
Answer: 20 × 10−17 kg m s−1
4. Let an electromagnetic wave propagate along the x direction, the magnetic field oscillates at a frequency of 1010 Hz and has an amplitude of 10−5T, acting along the y - direction. Then, compute the wavelength of the wave. Also write down the expression for electric field in this case.
Answer: λ = 3 × 10−18 m and E->( x,t) = 3 ×10 3 sin(2 . 09 ×1018 x −6 .28 ×1010 t)i ^ N C−1
5. If the relative permeability and relative permittivity of the medium is 1.0 and 2.25, respectively. Find the speed of the electromagnetic wave in this medium.
Answer: v = 2 m s−1
Displacement current and Maxwell’s correction to Ampere's circuital law:
EXAMPLE 5.1
Consider a parallel plate capacitor which is maintained at potential of 200 V. If the separation distance between the plates of the capacitor and area of the plates are 1 and 20 cm2. Calculate the displacement current for the time in µs.
Solution
Potential difference between the plates of the capacitor, V = 200 V
The distance between the plates,
d = 1 mm = 1 × 10-3 m
Area of the plates of the capacitor,
A = 20 cm2 = 20 × 10-4 m2
Time is given in micro-second, µs = 10-6 s
Displacement current
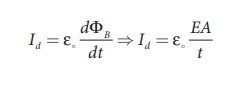
But electric field, E = V/d
Therefore,
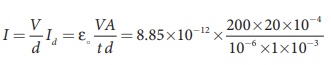
= 35400 ×10−7 = 3 .5 mA
Refractive index of the medium: Solved Example Problems
EXAMPLE 5.2
The relative magnetic permeability of the medium is 2.5 and the relative electrical permittivity of the medium is 2.25. Compute the refractive index of the medium.
Solution
Dielectric constant (relative permeability of the medium) is εr = 2.25
Magnetic permeability is µr = 2.5
Refractive index of the medium,
n = √ εrµr = √ [2 . 25 × 2.5] = 2.37
Sources of electromagnetic Waves: Solved Example Problems
EXAMPLE 5.3
Compute the speed of the electromagnetic wave in a medium if the amplitude of electric and magnetic fields are 3 × 104 N C-1 and 2 × 10-4 T, respectively.
Solution
The amplitude of the electric field, Eo = 3 × 104 N C-1
The amplitude of the magnetic field, Bo = 2 × 10-4 T. Therefore, speed of the electromagnetic wave in a medium is
= 3 ×104 / 2 ×10−4 = 1.5×108 ms−1
Electromagnetic spectrum
EXAMPLE 5.4
A magnetron in a microwave oven emits electromagnetic waves (em waves) with frequency f = 2450 MHz. What magnetic field strength is required for electrons to move in circular paths with this frequency?.
Solution
Frequency of the electromagnetic waves given is f = 2450 MHz
The corresponding angular frequency is
ω= 2πf = 2 x 3.14 x 2450 x 106
= 15,386 x 106 Hz
= 1.54 × 1010 s-1
The magnetic field B = meω / |q|
Mass of the electron, me = 9.22 x 10-31 kg
Charge of the electron
q =−1 . 60 ×10− 19 C ⇒ |q| = 1.60 ×10−19 C
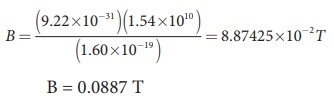
B = 0.0887 T
This magnetic field can be easily produced with a permanent magnet. So, electromagnetic waves of frequency 2450 MHz can be used for heating and cooking food because they are strongly absorbed by water molecules.
Related Topics