Maxwell’s equations in integral form

Maxwell’s equations in integral form

Electrodynamics can be summarized into four basic equations, known as Maxwell’s equations. These equations are analogous to Newton’s equations in mechanics. Maxwell’s equations completely explain the behaviour of charges, currents and properties of electric and magnetic fields. These equations can be written in integral form (or integration form) or derivative form (or differentiation form). The differential form of Maxwell’s equation is beyond higher secondary level because we need to learn additional mathematical operations like curl of vector fields and divergence of vector fields. So we focus here only in integral form of Maxwell’s equations:

1. First equation is nothing but the Gauss’s law. It relates the net electric flux to net electric charge enclosed in a surface. Mathematically, it is expressed as

where E is the electric field and Q_enclosed is the charge enclosed. This equation is true for both discrete or continuous distribution of charges. It also indicates that the electric field lines start from positive charge and terminate at negative charge. This implies that the electric field lines do not form a continuous closed path. In other words, it means that isolated positive charge or negative charge can exist.

2. Second equation has no name. But this law is similar to Gauss’s law in electrostatics. So this law can also be called as Gauss’s law in magnetism. The surface integral of magnetic field over a closed surface is zero. Mathematically,

where  is the magnetic field. This equation implies that the magnetic lines of force form a continuous closed path. In other words, it means that no isolated magnetic monopole exists.

3. Third equation is Faraday’s law of electromagnetic induction. This law relates electric field with the changing magnetic flux which is mathematically written as

where  is the electric field. This equation implies that the line integral of the electric field around any closed path is equal to the rate of change of magnetic flux through the closed path bounded by the surface. Our modern technological revolution is due to Faraday’s laws of electromagnetic induction. The electrical energy supplied to our houses from electricity board by using Faraday’s law of induction.

4. Fourth equation is modified Ampere’s circuital law. This is also known as Ampere – Maxwell’s law. This law relates the magnetic field around any closed path to the conduction current and displacement current through that path.

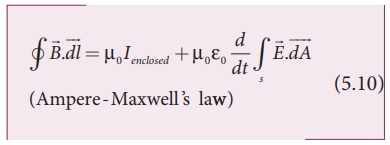
where  is the magnetic field. This equation shows that both conduction and also displacement current produces magnetic field. These four equations are known as Maxwell’s equations in electrodynamics. This equation ensures the existence of electromagnetic waves. The entire communication system in the world depends on electromagnetic waves. In fact our understanding of stars, galaxy, planets etc come by analysing the electromagnetic waves emitted by these astronomical objects.