Production and properties of electromagnetic waves - Hertz experiment

Electromagnetic Waves

Electromagnetic waves are non-mechanical waves which move with speed equals to the speed of light (in vacuum). It is a transverse wave. In the following subsections, we discuss the production of electromagnetic waves and its properties, sources of electromagnetic waves and also classification of electromagnetic spectrum.

Production and properties of electromagnetic waves - Hertz experiment

Maxwell’s prediction was experimentally confirmed by Heinrich Rudolf Hertz (Figure 5.7 (a)) in 1888. The experimental set up used is shown in Figure 5.7 (b).

It consists of two metal electrodes which are made of small spherical metals as shown in Figure 5.7. These are connected to larger spheres and the ends of them are connected to induction coil with very large number of turns. This is to produce very high electromotive force (emf). 

Since the coil is maintained at very high potential, air between the electrodes gets ionized and spark (spark means discharge of electricity) is produced. The gap between electrode (ring type – not completely closed and has a small gap in between) kept at a distance also gets spark. This implies that the energy is transmitted from electrode to the receiver (ring electrode) as a wave, known as electromagnetic waves. If the receiver is rotated by 90° - then no spark is observed by the receiver. This confirms that electromagnetic waves are transverse waves as predicted by Maxwell. Hertz detected radio waves and also computed the speed of radio waves which is equal to the speed of light (3 × 10⁸ m s^-1).

Properties of electromagnetic waves

1. Electromagnetic waves are produced by any accelerated charge.

2. Electromagnetic waves do not require any medium for propagation. So electromagnetic wave is a non-mechanical wave.

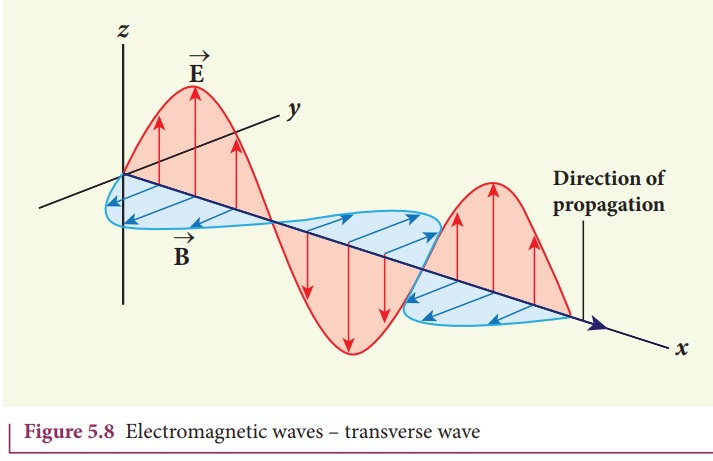
3. Electromagnetic waves are transverse in nature. This means that the oscillating electric field vector, oscillating magnetic field vector and propagation vector (gives direction of propagation) are mutually perpendicular to each other.

The electric and magnetic fields are in the y and z directions respectively and the direction of propagation is along x direction. This is shown in Figure 5.8.

4. Electromagnetic waves travel with speed which isequal to the speed of  light  in  vacuum  or  free  space,

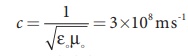 = 3x10⁸ ms^-1, where εo is the  permittivity of free space or vacuum and µ_o is the permeability of free space or vacuum (refer Unit 1 for permittivity and Unit 3 for permeability).

5. In a medium with permittivity ε and permeability µ, the speed of electromagnetic wave is less than speed in free space or vacuum, that is, < c. In a medium of refractive index,

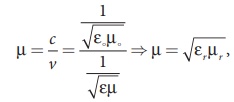
where ε_r is the relative permittivity of the medium (also known as dielectric constant) and µ_r is the relative permeability of the medium.

6. Electromagnetic waves are not deflected by electric field or magnetic field.

7. Electromagnetic waves can show interference, diffraction and can also be polarized.

8. The energy density (energy per unit volume) associated with an electromagnetic wave propagating in vacuum or free space is

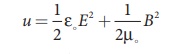
where, 1/2 ε E² = u_E  is the energy density in an electric field and 1/2µ₀ = B² = u_B is the energy density in a magnetic field.

Since, E = Bc ⇒ u_B = u_E.

The energy density of the electromagnetic wave is

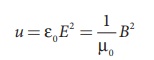
9. The average energy density for electromagnetic wave,

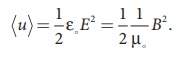
10. The energy crossing per unit area per unit time and perpendicular to the direction of propagation of electromagnetic wave is called the intensity.

11. Like other waves, electromagnetic waves also carry energy and momentum. For the electromagnetic wave of energy U propagating with speed c has linear momentum which

is given by = Energy / speed = U / c . The force exerted by an electromagnetic wave on unit area of a surface is called radiation pressure.

12. If the electromagnetic wave incident on a material surface is completely absorbed, then the energy delivered is U and momentum imparted on the surface is p = U/c .

13. If the incident electromagnetic wave of energy U is totally reflected from the surface, then the momentum delivered to the surface is ∆p

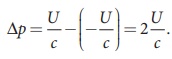
14. The rate of flow of energy crossing a unit area is known as pointing vector for electromagnetic waves, which is 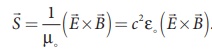. The unit for pointing vector is W m^-2. The pointing vector at any point gives the direction of energy transport from that point.

15. Electromagnetic waves carries not only energy and momentum but also angular momentum.

EXAMPLE 5.2

The relative magnetic permeability of the medium is 2.5 and the relative electrical permittivity of the medium is 2.25. Compute the refractive index of the medium.

Solution

Dielectric constant (relative permeability of the medium) is ε_r = 2.25

Magnetic permeability is µ_r = 2.5

Refractive index of the medium,

n = √ ε_rµ_r  = √ [2 . 25 × 2.5] = 2.37