Chemistry - Chemical Kinetics: Solved Example Problems | 12th Chemistry : UNIT 7 : Chemical Kinetics
Chapter: 12th Chemistry : UNIT 7 : Chemical Kinetics
Chemical Kinetics: Solved Example Problems
Molecularity: Solved Example Problems
Example 1
Consider the oxidation of nitric oxide to form NO2
2NO(g) + O2 (g) → 2NO2 (g)
(a). Express the rate of the reaction in terms of changes in the concentration of NO,O2 and NO2 .
(b). At a particular instant, when [O2] is decreasing at 0.2 mol L−1s−1 at what rate is [NO2 ] increasing at that instant?
Solution:
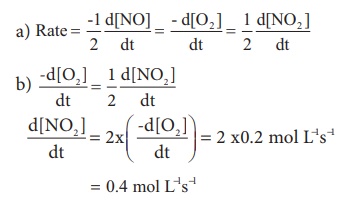
Evaluate yourself 1
1) Write the rate expression for the following reactions, assuming them as elementary reactions.
i) 3A + 5B2 →4CD
ii) X2 + Y2 →2XY
2). Consider the decomposition of N2O5 (g) to form NO2 (g) and O2 (g) . At a particular instant N2O5 disappears at a rate of 2.5x10-2 mol dm-3s-1 . At what rates are NO2 and O2 formed? What is the rate of the reaction?
Example 2
1. What is the order with respect to each of the reactant and overall order of the following reactions?
(a). 5Br− ( aq ) + BrO3−(aq ) + 6H+ (aq)
→ 3Br2 (l ) + 3H2O(l)
The experimental rate law is
Rate = k [Br− ][BrO3][H+]2
(b). CH3CHO(g ) →Δ→ CH4 (g) + CO(g)
the experimental rate law is
Rate = k [CH3CHO]3/2
Solution:
a) First order with respect to Br−, first order with respect to BrO3− and second order with respect to H+ . Hence the overall order of the reaction is equal to 1 + 1 + 2 = 4
b) Order of the reaction with respect to acetaldehyde is 3/2 and overall order is also 3/2
Example 3
2. The rate of the reaction x + 2y → product is 4 x 10−3 mol L−1s−1 if [x]=[y]=0.2 M and rate constant at 400K is 2 x 10-2 s-1 , What is the overall order of the reaction.
Solution :
Rate = k [x]n [y]m
4 x 10-3 mol L-1s-1 = 2 x 10-2 s-1 (0.2 mol L-1 )n (0.2mol L-1 )m
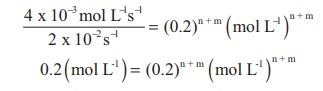
Comparing the powers on both sides
The overall order of the reaction n + m = 1
Evaluate yourself 2
1). For a reaction, X + Y → product ; quadrupling [x] , increases the rate by a factor of 8. Quadrupling both [x] and [y], increases the rate by a factor of 16. Find the order of the reaction with respect to x and y. what is the overall order of the reaction?
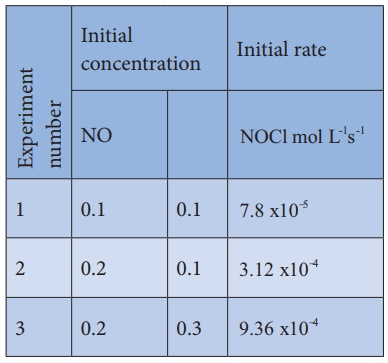
2). Find the individual and overall order of the following reaction using the given data.
2NO(g) + Cl2 (g) → 2NOCl(g)
Half life period of a reaction: Solved Example Problems
Example 4
A first order reaction takes 8 hours for 90% completion. Calculate the time required for 80% completion. (log 5 = 0.6989 ; log10 = 1)
Solution:
For a first order reaction,
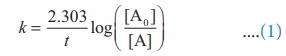
Let [A0 ] = 100M
When
t = t90% ; [A]=10M (given that t90 % =8hours)
t = t80% ; [A]=20M
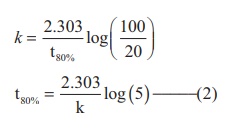
Find the value of k using the given data
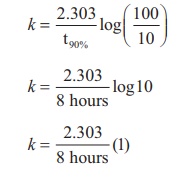
Substitute the value of k in equation (2)
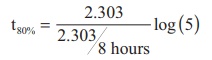
t80% = 8hours x 0.6989
t80% = 5.59hours
Example 5
(ii) The half life of a first order reaction x → products is 6.932 x 104s at 500K . What percentage of x would be decomposed on heating at 500K for 100 min. (e0.06 = 1.06)
Solution:
Given t1/2 = 0.6932 x 104 s
To solve :2 when t=100 min,
[ [A0 ] −[A] / [A0] ] x 100 = ?
We know that
For a first order reaction, t1/2 = 0.6932 / k

k = 10−5 s−1
Example 6
Show that in case of first order reaction, the time required for 99.9% completion is nearly ten times the time required for half completion of the reaction.

Evaluate yourself:
1. In a first order reaction A → products 60% of the given sample of A decomposes in 40 min. what is the half life of the reaction?
2. The rate constant for a first order reaction is 2.3 X 10 −4 s−1 If the initial concentration of the reactant is 0.01M . What concentration will remain after 1 hour?
3. Hydrolysis of an ester in an aqueous solution was studied by titrating the liberated carboxylic acid against sodium hydroxide solution. The concentrations of the ester at different time intervals are given below.
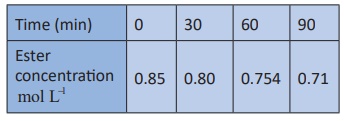
Show that, the reaction follows first order kinetics.
Arrhenius equation - The effect of temperature on reaction rate: Solved Example Problems
Example 7
The rate constant of a reaction at 400 and 200K are 0.04 and 0.02 s-1 respectively. Calculate the value of activation energy.
Solution
According to Arrhenius equation

Ea = 2305 J mol−1
Example 8
Rate constant k of a reaction varies with temperature T according to the following Arrhenius equation
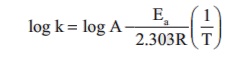
Where Ea is the activation energy. When a graph is plotted for log k Vs 1/T a straight line with a slope of - 4000K is obtained. Calculate the activation energy
Solution
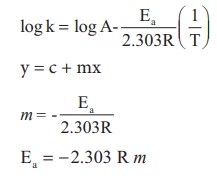
Ea = − 2.303 R m
Ea = − 2.303 x 8.314 J K−1 mol−1 x (− 4000K )
Ea = 76,589J mol−1
Ea = 76.589 kJ mol−1
Evaluate yourself
For a first order reaction the rate constant at 500K is 8 X 10−4 s−1 . Calculate the frequency factor, if the energy of activation for the reaction is 190 kJ mol-1 .
Chemical Kinetics - Example : Solved Example Problems
1. The rate law for a reaction of A, B and C hasbeenfoundtobe rate = k [ A]2 [B][L]3/2
How would the rate of reaction change when

(i) Concentration of [L] is quadrupled
Solution

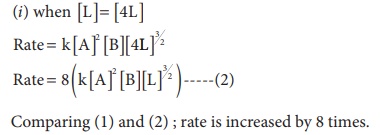
(ii) Concentration of both [A] and [B] are doubled
Solution

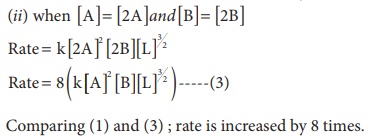
(iii) Concentration of [A] is halved
Solution

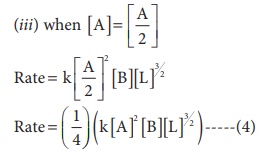
(iv) Concentration of [A] is reduced to(1/3) and concentration of [L] is quadrupled.
Solution

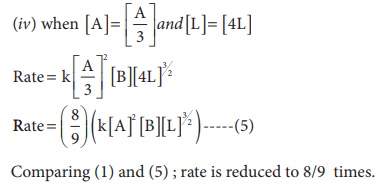
2. The rate of formation of a dimer in a second order reaction is 7.5 × 10−3 mol L−1s−1 at 0.05 mol L−1 monomer concentration. Calculate the rate constant.
Solution
Let us consider the dimerisation of a monomer M
2M → (M)2
Rate= k [M]n
Given that n=2 and [M] = 0.05 mol L-1
Rate = 7.5 X 10-3 mol L-1s-1
k = Rate/[M]n
k = 7.5x10-3/(0.05)2 = 3mol-1Ls-1
3. For a reaction x + y + z →products the rate law is given by rate = k [ x ]3/2 [ y ]1/2 what is the overall order of the reaction and what is the order of the reaction with respect to z.
Solution
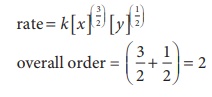
i.e., second order reaction.
Since the rate expression does not contain the concentration of z , the reaction is zero order with respect to z.
15. The decomposition of Cl2O7 at 500K in the gas phase to Cl2 and O2 is a first order reaction. After 1 minute at 500K, the pressure of Cl2O7 falls from 0.08 to 0.04 atm. Calculate the rate constant in s-1.
Solution

4. A gas phase reaction has energy of activation 200 kJ mol-1. If the frequency factor of the reaction is 1.6 × 1013 s−1 Calculate the rate constant at 600 K. ( e −40 .09 = 3.8 × 10−18 )
Solution
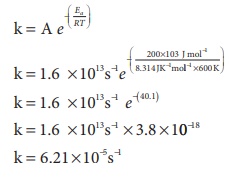
20. For the reaction 2x + y → L find the rate law from the following data.
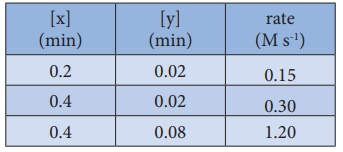
Solution
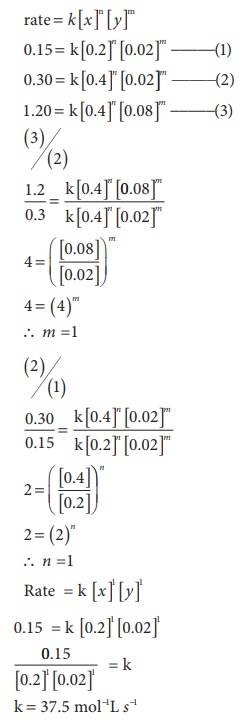
5. The rate constant for a first order reaction is 1.54 × 10-3 s-1. Calculate its half life time.
Solution
We know that, t1/2 = 0.693/ k
t1/2 = 0.693/1.54 x 10-3 s-1 = 450 s
6. The half life of the homogeneous gaseous reaction SO2Cl2 → SO2 + Cl2 which obeys first order kinetics is 8.0 minutes. How long will it take for the concentration of SO2Cl2 to be reduced to 1% of the initial value?
Solution
We know that, k = 0.693/ t1/2
k = 0.693/ 8.0 minutes= 0.087 minutes-1
For a first order reaction,
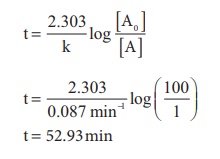
7. The time for half change in a first order decomposition of a substance A is 60 seconds. Calculate the rate constant. How much of A will be left after 180 seconds?
Solution

8. A zero order reaction is 20% complete in 20 minutes. Calculate the value of the rate constant. In what time will the reaction be 80% complete?
Solution
i) Let A = 100M, [A0]–[A] = 20M,
For the zero order reaction
k=([A0]-[A] / t)
k=(20M / 20min) = 1 Mmin-1
Rate constant for a reaction = 1Mmin-1
ii) To calculate the time for 80% of completion
k = 1Mmin-1, [A0] = 100M, [A0]-[A] = 80M, t = ?
Therefore
t=([A0]-[A] / k) = (80M / 1Mmin-1) = 80min
9. The activation energy of a reaction is 225 k Cal mol-1 and the value of rate constant at 40°C is 1.8 ×10−5 s−1 . Calculate the frequency factor, A.
Solution
Here, we are given that
Ea = 22.5 kcal mol-1 = 22500 cal mol-1
T = 40°C = 40 + 273 = 313 K
k = 1.8 × 10-5 sec-1
Substituting the values in the equation
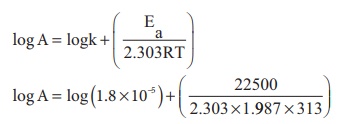
log A = log (1.8) −5 + (15.7089)
log A = 10.9642
A = antilog (10.9642)
A = 9.208 × 1010 collisions s−1
10. Benzene diazonium chloride in aqueous solution decomposes according to the equation C6H5N2Cl → C6H5Cl + N2 . Starting with an initial concentration of 10 g L−1 , the volume of N2 gas obtained at 50 °C at different intervals of time was found to be as under:
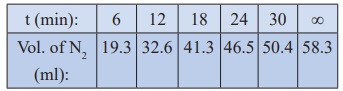
Show that the above reaction follows the first order kinetics. What is the value of the rate constant?
Solution
For a first order reaction
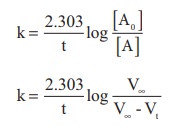
In the present case, V∞ = 58.3 ml.
The value of k at different time can be calculated as follows:
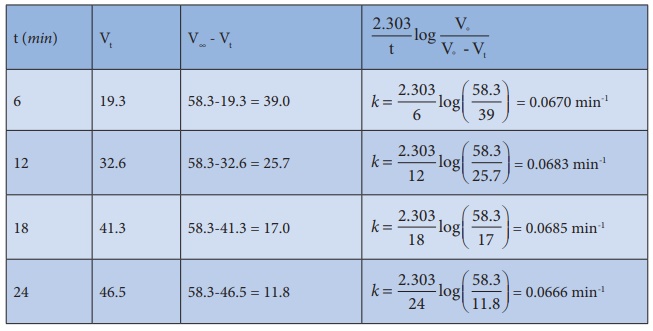
Since the value of k comes out to be nearly constant, the given reaction is of the first order. The mean value of k = 0.0676 min-1
11. From the following data, show that the decomposition of hydrogen peroxide is a reaction of the first order:

Where t is the time in minutes and V is the volume of standard KMnO4 solution required for titrating the same volume of the reaction mixture.
Solution
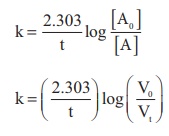
In the present case, Vo = 46.1 ml.
The value of k at each instant can be calculated as follows:

Thus, the value of k comes out to be nearly constant. Hence it is a reaction of the first order.
12. Where t is the time in minutes and V is the volume of standard KMnO4 solution required for titrating the same volume of the reaction mixture.
Solution
i) For the first order reaction k = 2.303/t log [A0]/[A]
Assume, [A0] = 100 %, t = 50 minutes
Therefore, [A] = 100 – 40 = 60
k = (2.303 / 50) log (100 / 60)
k = 0.010216 min-1
Hence the value of the rate constant is 0.010216 min-1
ii) t = ?, when the reaction is 80% completed,
[A] = 100 – 80 = 20%
From above, k = 0.010216 min-1
t = (2.303 / 0.010216) log (100 / 20)
t = 157.58 min
The time at which the reaction will be 80% complete is 157.58 min.
Related Topics