Chemical Kinetics - The integrated rate equation | 12th Chemistry : UNIT 7 : Chemical Kinetics
Chapter: 12th Chemistry : UNIT 7 : Chemical Kinetics
The integrated rate equation
The
integrated rate equation:
We have just learnt that
the rate of change of concentration of the reactant is directly proportional to
that of concentration of the reactant. For a general reaction,
A → product
The rate law is
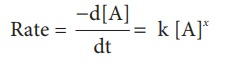
Where k is the rate
constant, and x is the order of the reaction. The above equation is a
differential equation, -d[A]/dt so it gives the rate at any instant. However,
using the above expression, we cannot answer questions such as how long will it
take for a specific concentration of A to be used up in the reaction? What will
be the concentration of reactant after a time ‘ t ’?. To answer such questions,
we need the integrated form of the above rate law which contains time as a
variable.
1. Integrated rate law for a first order reaction
A reaction whose rate
depends on the reactant concentration raised to the first power is called a
first order reaction. Let us consider the following Cl2 first order
reaction,
A → product
Rate law can be
expressed as
Rate = k [A]1
Where, k is the first
order rate constant.
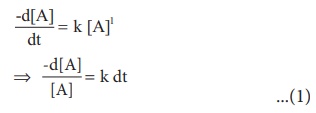
Integrate the above
equation between the limits of time t = 0 and time equal to t, while the
concentration varies from the initial concentration [A0 ] to [A] at
the later time.
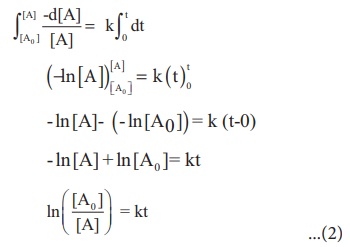
This equation is in
natural logarithm. To convert it into usual logarithm with base 10, we have to
multiply the term by 2.303.
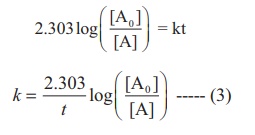
Equation (2) can be
written in the form y = mx + c as below
ln [A0 ] −ln [A] = kt
ln [A] = ln [A0 ] −kt
⇒
y = c + mx
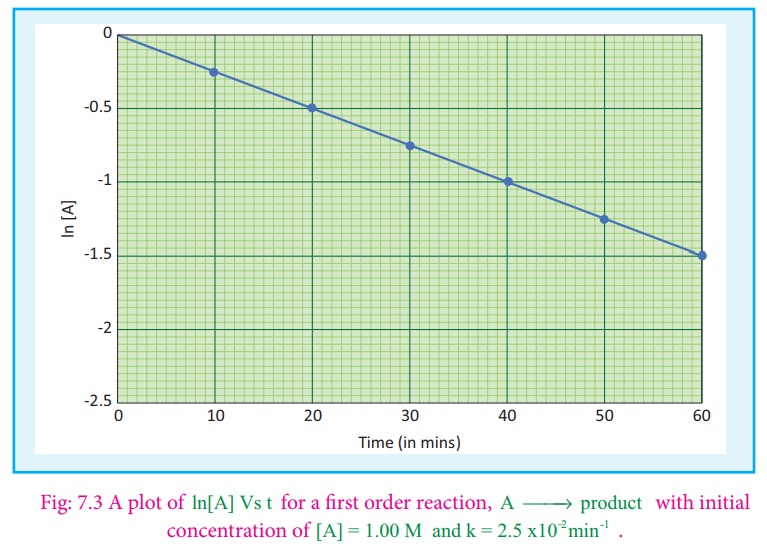
If we follow the
reaction by measuring the concentration of the reactants at regular time
interval‘t’, a plot of ln[A] against ‘t’ yields a straight line with a negative
slope.From this, the rate constant is calculated.
Examples for the first
order reaction
(i) Decomposition of
dinitrogen pentoxide
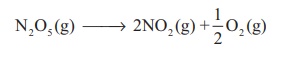
(ii) Decomposition of
thionylchloride; SO2Cl2 (l) →SO2 (g) + Cl2
(g)
(iii) Decomposition of
the H2O2 in
aqueous solution; H2O2 (aq) → H2O(l) + ½ O2(g)
(iv) Isomerisation of cyclopropane to propene.
Pseudo first order reaction:
Kinetic study of a
higher order reaction is difficult to follow, for example, in a study of a
second order reaction involving two different reactants; the simultaneous
measurement of change in the concentration of both the reactants is very
difficult. To overcome such difficulties, A second order reaction can be
altered to a first order reaction by taking one of the reactant in large
excess, such reaction is called pseudo first order reaction. Let us consider
the acid hydrolysis of an ester,
CH3 COOCH3
(aq) + H2 O (l) → H + → CH3COOH (aq)
+ CH3OH (aq)

Rate = k [CH3
COOCH3 ] [H2O]
If the reaction is
carried out with the large excess of water, there is no significant change in
the concentration of water during hydrolysis. i.e.,concentration of water
remains almost a constant.
Now, we can define k [H2O]
= k' ; Therefore the above rate equation becomes
Rate = k' [CH3COOCH3
]
Thus it follows first
order kinetics.
2. Integrated rate law for a zero order reaction:
A reaction in which the
rate is independent of the concentration of the reactant over a wide range of
concentrations is called as zero order reactions. Such reactions are rare. Let
us consider the following hypothetical zero order reaction.
A→product
The rate law can be
written as,
Rate = k [A]0
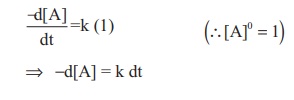
Integrate the above equation between
the limits of [A0] at zero time and [A] at some later time 't',
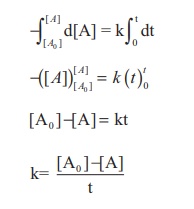
Equation (2) is in the
form of a straight
line y = mx + c
Ie., [A] = −kt + [A0 ]
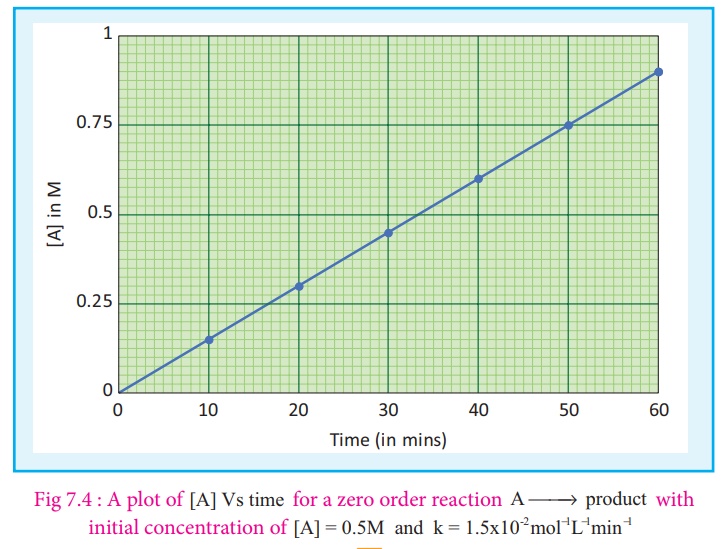
y = c + mx
A plot of [A] Vs time
gives a straight line with a slope of −k
and y - intercept of
[A0 ] .
Examples for a zero order reaction:
1. Photochemical reaction
between H2 and I2
H2 (g)+Cl2
(g) →hv→2HCl(g)
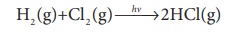
2. Decomposition of N2O
on hot platinum surface
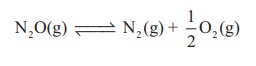
3. Iodination of acetone in acid medium is zero order with respect
to iodine.
CH3COCH3
+ I2 →H →ICH2COCH3
+ HI
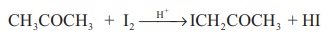
Rate = k [CH3COCH3
] [H+ ]

Related Topics