Book Back and Important Questions Answers - Chemical Kinetics: Answer the following questions | 12th Chemistry : UNIT 7 : Chemical Kinetics
Chapter: 12th Chemistry : UNIT 7 : Chemical Kinetics
Chemical Kinetics: Answer the following questions
Chemical Kinetics
Answer the following questions:
1. Define average rate and instantaneous rate.
• The average rate of a reaction is
defined as the rate of change of concentration of a reactant (or a product)
over a specified measureable period of time.
• The rate of the reaction, at a
particular instant during the reaction is called the instantaneous rate.
2. Define rate law and rate constant.
Rate
law is an expression which relates the rate of a reaction with rate constant
and concentration of reacting substances.
xA
+ yB → products
• The rate law for the above
reaction is
Rate
= k [A]m [B]n
• where k is a proportionality
constant.
• Rate
constant is equal to the rate of reaction, when the concentration of
each of the reactants in unity.
• It does not depend on the initial
concentration of reactants.
3. Derive integrated rate law for a zero order reaction A → product .
A reaction in which the rate is independent of
the concentration of the reactant over a wide range of concentrations is called
as zero order reactions.
A
→ product
The
rate law can be written as,
Rate
= k[A]0
−
d [A] / dt = k(l)
−
d [A] = kdt
Integrate
the above equation between the limits of [A0] at zero time and [A]
some later time ' t'
−ʃ[A][A0] d [A] = k ʃt0 dt
[A0]
− [A] = kt
k = {
[A0] – [A] } / t
[A] = − kt + [A0] is in the form of
straight line equation.
A
plot of [A] vs time gives a straight line with a slope of −k and y intercept of
[A0]
4. Define half life of a reaction. Show that for a first order reaction half life is independent of initial concentration.
The
half life of a reaction is defined as the time required for the reactant
concentration to reach one half its initial value.
For
a first order reaction, the half life is a constant i.e., it does not depend on
the initial concentration
The
rate constant for a first order reaction is given by
k = 2.303/t log {[A0]/[A]}
At
t = t1/2 ;
[A]
= [A0] / 2
k =2.303/t1/2
log {[A0] / [A0 /2]}
k = { 2.303
/ t1/2 } log (2)
k
= [2.303 × 0.3010] / t1/2 = 0.6932 / t1/2
t1/2
= 0.6932 / k
There
is no concentration term involved in the equation. Hence half life is
independent of initial concentration.
5. What is an elementary reaction? Give the differences between order and molecularity of a reaction.
Each
and every single step in a reaction mechanism is called elementary reaction.
An
elementary step is characterized by its molecularity.

Order of reaction
1.
It is the sum of the powers of concentration terms involved in the experimentally
determined rate law.
2.
It can be zero (or) fractional (or) integer.
3.
It is assigned for a overall reaction
Molecularity of a reaction
1. It is the total number of reactant
species that are involved in an elementary step.
2.
It is always whole number, can not be zero or a fractional number.
3.
It is assigned for each elementary step of mechanism.
6. Explain the rate determining step with an example.
Slowest
step is the rate determining step in the series of chemical reaction which
occurs simultaneously.
The
decomposition of hydrogen peroxide catalysed by I−.
2H2O2(aq)
→ 2H2O(l) + O2(g)
It
is experimentally found that the reaction is first order with respect to both H2O2
and I−, which indicates that I− is also involved in the
reaction. The mechanism involves the following steps.
Step: 1
H2O2(aq)
+ I−(aq) → H2O(l)
+ OI−(aq)
Step: 2
2H2O2
(aq) + 2OI− (aq) → 2H2O(Ɩ) + O2(g) + I2
These
two reactions are elementary reactions. Adding the equations give the overall
reaction. Step 1 is the rate determining step, since it involves both H2O2
and I−, the overall reaction is bimolecular.
7. Describe the graphical representation of first order reaction.
k = 1/t Ɩog
{[A0] / [A]}
On
rearranging kt = ln[A0] − In [A]
This
equation is in the form of straight line
y = c + mx
ln[A0]
- ℓn[A] = kt
ln[A]
= ln[A0] - kt
A
plot of ln[A] against 't' yields a
straight line with a negative slope.

From
the slope the rate constant (k) is calculated.
8. Write the rate law for the following reactions.
a. A reaction that is 3/2 order in x and zero order in y.
b. A reaction that is second order in NO and first order in Br2.
Answer:
a)
r
= k [x]3/2 [y]0
r
= k [x]3/2
b) r =
k[NO]2 [Br2]
9. Explain the effect of catalyst on reaction rate with an example.
A
significant changes in the reaction can be brought out by the addition of a
catalyst. A catalyst is substance which alters the rate of a reaction without
itself undergoing any permanent chemical change. In the presence of a catalyst,
the energy of activation is lowered and hence, greater number of molecules can
crosses the energy barrier and change over to products, there by increasing the
rate of the reaction.
10. The rate law for a reaction of A, B and C has been found to be rate = k [ A]2 [B][L]3/2
How would the rate of reaction change when
Rate = k [ A]2 [B][L]3/2 ............(1)
(i) Concentration of [L] is quadrupled
Solution
Rate
= k[A]2 [B][L]3/2 ………….(1)
(i) When [L]
= [4L]
Rate
= k[A]2[B][4L]3/2
Rate
= 8(k[A]2 [B] [L]3/2) ………… (2)
Comparing
(1) and (2); rate is increased by 8 times
(ii) When [A]
= [2A] and [B] = [2B]
Rate
= k[2A]2 [2B] [L]3/2
Rate
= 8(k[A]2 [B][L]3/2)……………. (3)
Comparing
(1) and (3); rate is increased by 8 times.
(iii) when [A]
= [A/2]
Rate
= k[A/2]2 [B] [L]3/2
Rate
= (1/4) (k[A]2 [B] [L]3/2) …………..(4)
Comparing
(1) and (4); rate is reduced to 1/4 times.
(iv) When [A]
= [A/3] and [L] = [4L]
Rate
= k[A/3]2 [B] [4L]3/2
Rate = (8/9) (k[A]2 [B] [L]3/2) ……….(5)
11. The rate of formation of a dimer in a second order reaction is 7.5 × 10−3 mol L−1s−1 at 0.05 mol L−1 monomer concentration. Calculate the rate constant.
Solution
Let
us consider the dimerisation of a monomer M
2M
_____→ (M)2
Rate
= k[M]n
Given
that n = 2 and [M] = 0.05 mol L−1
Rate
= 7.5 × 10−3 mol L−1 s−1
k
= Rate / [M]n
k
= 7.5×10−3 / (0.05)2 = 3 mol−1 Ls−1
12. For a reaction x + y + z →products the rate law is given by rate = k [ x ]3/2 [ y ]1/2 what is the overall order of the reaction and what is the order of the reaction with respect to z.
Solution
Rate
= k[x](3/2) [y](1/2)
Overall
order = (3/2 +1/2) = 2
ie.,
second order reaction.
since the rate expression does not contain the concentration of Z, the reaction is zero order with respect to Z..
13. Explain briefly the collision theory of bimolecular reactions.
• Collision theory is based on the
kinetic theory of gases.
• According to this theory,
chemical reactions occur as a result of collisions between the reacting
molecules.
A2(g)
+ B2(g) → 2AB(g)
The
reaction between A2 and B2 molecules proceeds through
collisions between them, then the rate would be proportional to the number of
collisions per second.
• Rate α number of molecules
colliding per liter per second (collision rate)
• The number of collision is
directly proportional to the concentration of both A2 and B2
Collision
rate ∝ [A2] [B2]
Collision
rate = Z [A2] [B2]
Where
Z is a constant.
• All collisions are not effective
to lead the reaction. In order to react, the colliding molecules must possess a
minimum energy called activation energy.
• The molecules that collide with
less energy than activation energy will remain interact and no reaction occurs
• Fraction of effective collisions
(f) is given by the following expression
f
= e-Ea/RT
The
fraction of collision is further reduced due to orientation factor .i.e., even
if the reactant collide with sufficient energy, they will not react unless the
orientation of the reactant molecules is suitable for the formation of the
transition state.
The
fraction of effective collision (f) having the proper orientation is given by
the steric factor P.
→
rate = P × f × collision rate
i.e.,
rate = p × e−Ea/RT × Z [A2] [B2] …………1
As
per the rate law,
Rate
= k [A2] [B2] …………………….2
Where
k is the constant
k
= pZe−Ea/RT
14. Write Arrhenius equation and explains the terms involved.
Arrhenius
suggested that the rates of reactions vary with temperature in such a way that
the rate constant is directly proportional to e−Ea/RT and he
proposed a relation between the rate constant and temperature.
k
= Ae−Ea/RT
Where
A the frequency factor
R
gas constant
Ea
the activation energy of the reaction
T the absolute temperature (in K)
A
is the frequency factor
15. The decomposition of Cl2O7 at 500K in the gas phase to Cl2 and O2 is a first order reaction. After 1 minute at 500K, the pressure of Cl2O7 falls from 0.08 to 0.04 atm. Calculate the rate constant in s-1.
Solution
k = 2.303/t log ([A0] / [A])

k
= (2.303 /1 min) log {[0.08] / [0.04]}
k
= 2.303 log 2
k = 2.303 × 0.3010
k
= 0.6932 min−1
k
= (0.6932/60) S−1
k = 1.153×10-2s−1
16. Explain pseudo first order reaction with an example.
A
second order reaction can be altered to a first order reaction by taking one of
the reactant in large excess, such reaction is called pseudo first order
reaction.
Let
us consider the acid hydrolysis of an ester.
CH3COOCH3
(aq) + H2O(ℓ) → CH 3COOH (aq) + CH3
OH(aq)
Rate
= k [CH3COOCH3] [H2O]
If
the reaction is carried out with the large excess of water, there is no
significant change in the concentration of water during hydrolysis .i.e.,
concentration of water remains almost a constant.
k
[H2O] = k'
There
fore the above rate equation becomes
Rate
= k' [CH3COOCH3]
Thus
it follows first order kinetics
17. Identify the order for the following reactions
(i) Rusting of Iron
(ii) Radioactive disintegration of 92 U238
(iii) 2 A + 3B → products ; rate = k [ A]1/2 [B ]2
Answer:
i)
Theoretically order value may be more than one but practically one.
ii)
I order
iii)
(1/2 +2) = 5/2
18. A gas phase reaction has energy of activation 200 kJ mol-1. If the frequency factor of the reaction is 1.6 × 1013 s−1 Calculate the rate constant at 600 K. ( e −40 .09 = 3.8 × 10−18 )
Solution:
k
= A e −Ea
k
= 1.6×1013 s−1 e
− (200x103 J / mol−1 / 8.314 JK−1
mol−1 × 600 K)
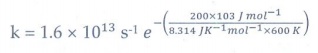
k
= 1.6 × 1013 s−1 e− (40.1)
k
= 1.6 × 1013 s−1 × 3.8 × 10−18
k
= 6.21 × 10-5 s−1
19. For the reaction 2x + y → L find the rate law from the following data.

Solution
Rate
= k[x]n [y]m
0.15
= k [0.2]n [0.02]m ……….. .….(1)
0.30
= k [0.4]n [0.02]m …………. (2)
1.20
= k [0.4]n [0.08]m ………….. (3)
(3)
/ (2)
1.2
/ 0.3 = k[0.4]n[0.08]m
/ k[0.4]n [0.02]m
4
= ([0.08] / [0.02])m
4
= (4)m
∴ m = l
(2)
/ (l)
0.30
/ 0.15 = { k[0.4]n [0.02]m
} / { k[0.2]n [0.02]m}
2
= ([0.4] / [0.2])n
∴ n = 1
Rate
= k [x]1 [y]1
0.15
= k [0.2]1 [0.02]1
0.15
/ {[0.2]1 [0.02]1} =
k
k = 37.5 mol−1 Ls−1
20. How do concentrations of the reactant influence the rate of reaction?
The
rate of a reaction increases with increase in the concentration of the
reactants. The effect of concentration is explained on the basis of collision
theory, the rate of reaction depends upon the number of collisions between the
reacting molecules. Higher the concentration, greater is possibility for
collision and hence the rate.
21. How do nature of the reactant influence rate of reaction.
A
chemical reaction involves breaking of certain existing bonds of the reactant
and forming new bonds which lead to the product.
The
physical state of the reactant is an important role to influence the rate of
reactions.
Gas
Phase Reactions are faster as compared to the reactions involving solid or
liquid reactants.
22. The rate constant for a first order reaction is 1.54 × 10-3 s-1. Calculate its half life time.
Solution
t
1/2 = 0.693 / k
t
1/2 = 0.693 / k
t
1/2 = 0.693 / 1.54 × 10−3 s−1 = 450 s
23. The half life of the homogeneous gaseous reaction SO2Cl2 → SO2 + Cl2 which obeys first order kinetics is 8.0 minutes. How long will it take for the concentration of SO2Cl2 to be reduced to 1% of the initial value?
Solution:
k
= 0.693 / t1/2
k
= 0.693 / 8.0 minutes = 0.087 minutes−1
For
a first order reaction,
t
= 2.303/k log ([A0]/[A])
t
= 2.303 / 0.087 min−1 log (100/1)
t = 52.93 min
24. The time for half change in a first order decomposition of a substance A is 60 seconds. Calculate the rate constant. How much of A will be left after 180 seconds?
Solution:
i)
Order of a reaction = 1;
t1/2
= 60 seconds,
k = ?
We
know that, k = 2.303 / t1/2
k
= 2.303/60 = 0.01155 s−1
ii)
[A0] = 100% t =180 s, k = 0.01155 s−1, [A] = ?
For
the first order reaction k = 2.303/t log(100/[A])
[
0.01155 × 180 ] / 2.303 = log (100/[A])
0.9207
= log 100 − log [A]
log [A] = log 100 - 0.9207
log [A] = 2 - 0.9207
log
[A] = 1.0973
[A]
= antilog of (1.0973)
[A] = 12.5 %
25. A zero order reaction is 20% complete in 20 minutes. Calculate the value of the rate constant. In what time will the reaction be 80% complete?
Solution
i) Let A = 100M, [A0]–[A] = 20M,
For the zero order reaction
k=([A0]-[A] / t)
k=(20M / 20min) = 1 Mmin-1
Rate constant for a reaction = 1Mmin-1
[or]
A
= 100%, x = 20%, Therefore,
a
− x = 100 − 20 = 80
For
the zero order reaction k =(x/t)
k
= (20/20) = 1
Rate
constant for a reaction = 1
ii) To calculate the time for 80% of completion
k = 1Mmin-1, [A0] = 100M, [A0]-[A] = 80M, t = ?
Therefore
t=([A0]-[A] / k) = (80M / 1Mmin-1) = 80min
26. The activation energy of a reaction is 225 k Cal mol-1 and the value of rate constant at 40°C is 1.8 ×10−5 s−1 . Calculate the frequency factor, A.
Solution
Here,
we are given that
Ea
= 22.5 kcal mo1−1 = 22500 cal mo1−1
T
= 40°C = 40 + 273 = 313 K
k
= 1.8 × 10−5 sec−1
Substituting
the values in the equation
log
A = logk + (Ea/2.303RT)
log
A = log (1.8 × 10−5) + (22500 / [2.303 × 1987 × 313])
log
A = log (1.8) - 5 + (15.7089)
log
A = 10.9642
A
= antilog (10.9642)
A
= 9.208 × 1010 collisions s−1
27. Benzene diazonium chloride in aqueous solution decomposes according to the equation C6H5N2Cl → C6H5Cl + N2 . Starting with an initial concentration of 10 g L−1 , the volume of N2 gas obtained at 50 °C at different intervals of time was found to be as under:
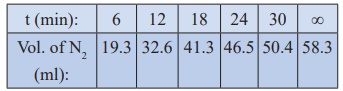
Show that the above reaction follows the first order kinetics. What is the value of the rate constant?
Solution:
For
a first order reaction
k
= 2.303/t log [a / (a-x)]
k
= 2.303/t log [V∞/V∞-Vt]
In
the present case, V∞ =
58.3 ml.
The
value of k at different time can be calculated as follows:
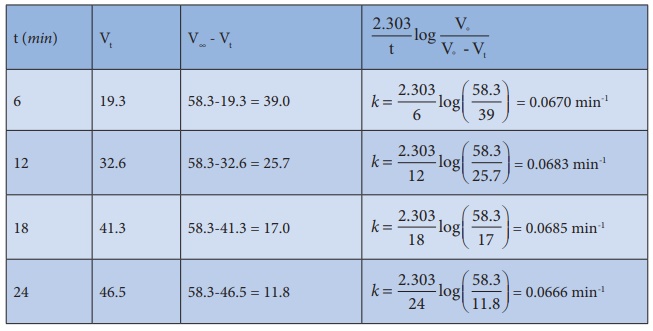
Since the value of k comes out to be nearly constant, the given reaction is of the first order. The mean value of k = 0.0676 min-1
28. From the following data, show that the decomposition of hydrogen peroxide is a reaction of the first order:

Where t is the time in minutes and V is the volume of standard KMnO4 solution required for titrating the same volume of the reaction mixture.
Solution:
Volume
of KMnO4 solution used ∞ amount of H2O2
present. Hence if the given reaction is of the first order, it must obey the
equation.
k
= 2.303/t log [a/(a-x)]
k=
(2.303/t) log (V0 /Vt)
In
the present case, V0 = 46.1 ml.
The value of k at each instant can be calculated as follows:

Thus, the value of k comes out to be nearly constant. Hence it is a reaction of the first order.
29. A first order reaction is 40% complete in 50 minutes. Calculate the value of the rate constant. In what time will the reaction be 80% complete?
Solution
i) For the first order reaction k = 2.303/t log [A0]/[A]
Assume, [A0] = 100 %, t = 50 minutes
Therefore, [A] = 100 – 40 = 60
k = (2.303 / 50) log (100 / 60)
k = 0.010216 min-1
Hence the value of the rate constant is 0.010216 min-1
ii) t = ?, when the reaction is 80% completed,
[A] = 100 – 80 = 20%
From above, k = 0.010216 min-1
t = (2.303 / 0.010216) log (100 / 20)
t = 157.58 min
The time at which the reaction will be 80% complete is 157.58 min.
i)
For the first order reaction k = 2.303/t
log [a / a-x]
Assume,
a = 100%, x = 40%, t = 50 minutes
Therefore,
a−x = 100 − 40 = 60
k
= (2.303 /50) log (100/60)
k
= 0.010216 min−1
Rate
constant = 0.010216 min−1
ii)
t = ?, when x = 80%
Therefore,
a−x = 100 − 80 = 20
From
above, k = 0.010216 min−1
t
= (2.303 / 0.010216) log (100/20)
t
= 157.58 min
The time at which the reaction will be 80% complete is 157.58 min.
SELF EVALUTION:
1. Write the rate
expression for the following reactions, assuming them as elementary reactions.
i) 3A + 5B2 → 4CD
ii) X2 + Y2
→ 2XY
Answer:
i)
3A + 5B2 → 4CD
Rate
= − 1/3 {d [A]/dt} =1/5 {d[B2]/dt} = 1/4 {d [CD]/dt}
X2
+ Y2 → 2XY
ii)
− d[X2] / dt = − d[Y2]
/ dt = 1/2 {d[XY]/dt}
= Rate
2. Consider the
decomposition of N2O5(g) to form NO2(g) and O2(g).
At a particular instant N2O5 disappears at a rate of 2.5
× 10-2 mol dm−3 s−1. At what rates are NO2
and O2 formed? What is the rate of the reaction?
Answer:
2 N2O5(g) → 4NO2(g)
+ O2(g)
Rate
= 1/2 {d [N2O5]
/ dt} = −1/4 {d [NO2] / dt } = d[O2] / dt
Rate
of disappearance,
of
N2O5 = 2.5 × 10−2 mol dm−3s−1
−(1/2)
{ d [N2O5]
/ dt } =1/4 {d [NO2] / dt}
d [NO2] / dt = 4/2{ − [ d [N2O5] / dt]}
=
2 × 2.25 × 10-2 mol dm−3 s−1
d [NO2] / dt = 5.0 × 10−2 mol dm−3 s−1
d [O2] / dt = − 1/2 [ d [N2O5] / dt ]
=
1/2 × 2.5 × 10−2 mol dm−3 s−1
d [O2] / dt = 1.25 × 10−2 mol dm−3 s−1
3. For a reaction,
X + Y → product; quadrupling [x], increase the rate by a factor of 8.
Quadrupling both [x] and [y], increases the rate by a factor of 16. Find the
order of the reaction with respect to x and y. What is the overall order of the
reaction?
Answer:
k
= [x]a [y]b = R ……………… 1
Quadrupling
[x]
k
= [4x]a [y]b = 8R ……………….2
Quadrupling
both [x] and [y]
k
= [4x]a [4y]b = 16R ………………..3
Divide
3/2
[
k[4x]a [4y]b ] / [ k[4x]a [y]b ] = 16R / 8R
4b
=(4)1/2
b = 1/2 order
order
with respect to y = 1/2
Divide
2/1
{
k[4x]a [4y]b } / { k[x]a [y]b } = 8R / R
4a = 8
4a = 43/2
a = 3/2
Over
all order 3/2 + 1/2 = 2.
4. Find the
individual and overall order of the following reaction using the given data.
2NO(g)
+ Cl2(g) → 2NOCl(g)

Answer:
Rate
= k [NO]m [Cl2]n
for
experiment 1
Rate1
= k [NO]m [Cl2]n
7.8
× 10--5= k[0.1]m
[0.1]n ………….1
for
experiment 2
Rate1
= k [NO]m [Cl2]n
3.12
× 10-4 = k[0.2]m
[0.1]n ……………. 2
for
experiment 3
9.36
× 10-4 = k[0.2]m
[0.3]n ……………. 3
2/1
⇒ [ 3.12 × 10-4 ] / [ 7.8
× 10-5 ] = [ k [0.2]m[0.l]n ] / [ k
[0.1]m [0.l]n ]
4
= (0.2/0.1) m
4
= (2)m
(2)2
= (2)m
m
=2
3/2
= [ 9.36 × 10 -4 ] / [ 3.12 × 10 -4 ] = [ k[0.2]m
[0.3]n ] / [ k [0.2]m
[0.1]n ]
3=
(3)n
n
=1
The
reaction is II order with respect to NO, I order with respect to Cl2
Over
all order = 3
Rate
= k [NO]1 [Cl2]2
Alternate method
Compare
experiment 1 and 2 concentration of Cl2 is constant, and the
concentration of NO doubled. When [NO] is doubled rate increased to four times.
Hence II order with respect to [NO]
Compare
experiment 2 and 3 concentration of NO is constant and the concentration of Cl2
is three time increased.
When
[Cl2] increased three times, the rate also increased three times.
Hence I order with respect to [Cl2]
Total
order III
5. In a first order
reaction A → products 60% of the given sample of A decomposes in 40 min. What
is the half life of the reaction?
Answer:
For
I order reaction
k
= 2.303/t log {[A0]/[A]}
t
= 40 min
[A0]
= 100%
[A] = 60%
k
= 2.303/40 log{100/60} = 0.01277
t1/2
= 0.693 / k
t1/2
= 0.693 / 0.01277 = 50.03
t1/2
= 50 min
6. The rate
constant for a first order reaction is 2.3 x10- 4 s−1 if
the initial concontration of the reactant is 0.01 M. What concentration will
remain after 1 hour?
Answer:
k
= 2.3 × 10−4 s−1
k
= (2.303) / (1×60×60) log ([0.01]/[A])
(2.3
× 10-4 × 60 × 60) / (2.303) = log 0.01- log [A]
0.3595
= −2 − log [A]
2.3595
= − log [A]
log [A] = − 2.3595
[A]
= Antilog [−2.3595]
[A] = 4.370 × 10−3
7. Hydrolysis of an ester in an aqueous solution was studied by titrating the liberated carboxylic acid against sodium hydroxide solution. The concentrations of the ester at different time intervals are given below:

Show that, the reaction follows
first order kinetics.
Answer:
Hydrolysis
of an ester in aqueous solution follows pseudo first order reaction. Water
taken as excess amount hence it is constant.
k
= 2.303/t log co/c
Co
= 0.85 mol l−1

k1
= 2.303/30 log (0.85/0.80) = 2.02 × 10−3
k2
= 2.303 / 60 log (0.85/0.754) = 1.99 × 10 −3
K3
= 2.303 / 90 log (0.85/0.71) = 2.00 × 10 −3
Since
the value of k comes out to be nearly constant, the given reaction of the first
order. The mean value of k = 2.00 × 10−3 min−1
8. For a first
order reaction the rate constant at 500 K is 8 × 10-4 s−1.
Calculate the frequency factor, if the energy of activation for the reaction is
190 kJ mol−1
Answer:
k
= 8 × l0-4 s−1
T
= 500K
Ea=
190 kJ mol−1
A=?
k
= Ae−Ea/RT
A
= k / [e – Ea /RT] = [8 × 10-4 s−1 ] / [e−{190000
/ 8.314×500}]
[8x10−4
] / [ 1.41 × 10−20 ] = 5.67 × 106
Related Topics