Rate of a chemical reaction

Rate of a chemical reaction:

A rate is a change in a particular variable per unit time. You have already learnt in physics that change in the displacement of a particle per unit time gives its velocity. Similarly in a chemical reaction, the change in the concentration of the species involved in a chemical reaction per unit time gives the rate of a reaction.

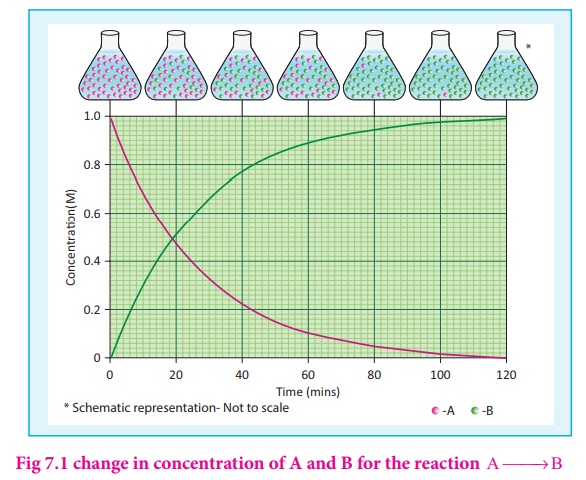
Let us consider a simple general reaction

A→ B

The concentration of the reactant ([A]) can be measured at different time intervals. Let the concentration of A at two different times t₂ and t₂ , (t₂>t₁) be [A₁] and [A₂] respectively. The rate of the reaction can be expressed as

During the reaction, the concentration of the reactant decreases i.e. [A₂ ] < [A₁] and hence the change in concentration [A₂ ] - [A₁] gives a negative value. By convention the reaction rate is a positive one and hence a negative sign is introduced in the rate expression (equation 7.1)

If the reaction is followed by measuring the product concentration, the rate is given by (Δ[B] / Δ t) since [B ]>[B ] 2 1 , no minus sign is required here.

Unit of rate of a reaction:

unit of rate = unit of concentration  / unit of time

Usually, concentration is expressed in number of moles per litre and time is expressed in seconds and therefore the unit of the rate of a reaction is mol L-1s-1 . Depending upon the nature of the reaction, minute, hour, year etc can also be used.

For a gas phase reaction, the concentration of the gaseous species is usually expressed in terms of their partial pressures and in such cases the unit of reaction rate is atm s-1 .

1. Stoichiometry and rate of a reaction:

In a reaction A → B , the stoichiometry of both reactant and product are same, and hence the rate of disappearance of reactant (A) and the rate of appearance of product (B) are same.

Now, let us consider a different reaction

 A→2B

In this case, for every mole of A, that disappears two moles of B appear, i.e., the rate of formation of B is twice as fast as the rate of disappearance of A. therefore, the rate of the reaction can be expressed as below

For a general reaction, the rate of the reaction is equal to the rate of consumption of a reactant (or formation of a product) divided by its coefficient in the balanced equation

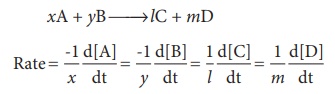
2. Average and instantaneous rate:

Let us understand the average rate and instantaneous rate by considering the isomerisation of cyclopropane.

The kinetics of the above reaction is followed by measuring the concentration of cyclopropane at regular intervals and the observations are shown below. (Table 7.1)

Table 7.1 Concentration of cyclopropane at various times during its isomerisation at 780K

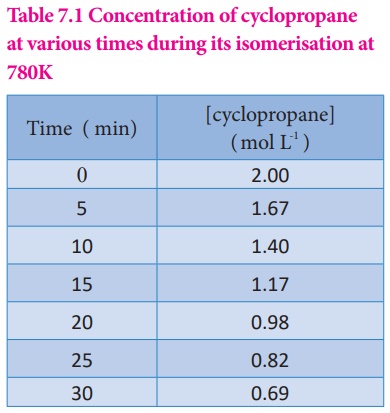
It means that during the first 30 minutes of the reaction, the concentration of the reactant ( cyclo propane) decreases as an average of 4.36 × 10^-2 mol L^-1 each minute.

Let us calculate the average rate for an initial and later stage over a short period.

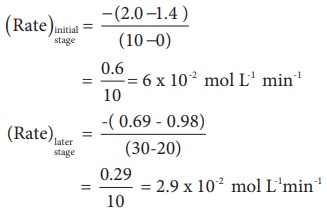
From the above calculations, we come to know that the rate decreases with time as the reaction proceeds and the average rate cannot be used to predict the rate of the reaction at any instant. The rate of the reaction, at a particular instant during the reaction is called the instantaneous rate. The shorter the time period, we choose, the closer we approach to the instantaneous rate,

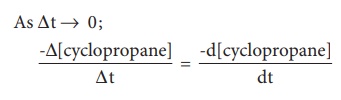
A plot of [cyclopropane] Vs (time) gives a curve as shown in the figure 7.2. Instantaneous rate at a particular instant ‘t ’ -d [cyclopropane] / dt the slope of a tangent drawn to the curve at that instant.

In general, the instantaneous reaction rate at a moment of mixing the reactants is calculated from the slope of the tangent drawn to the curve at mol L-1 , the rate calculated by this method is called initial rate of a reaction.

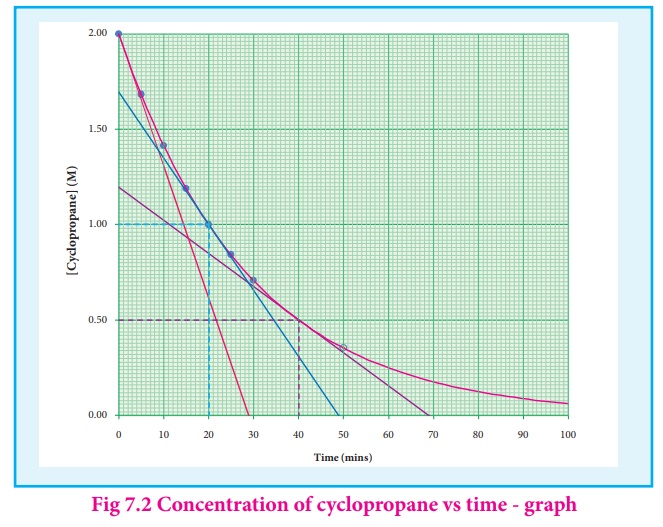
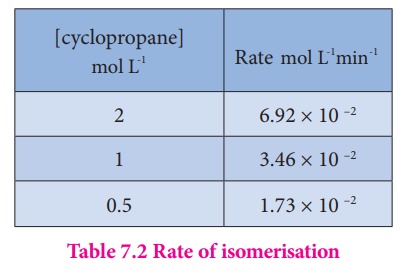
Let us calculate the instantaneous rate of isomerisation cyclopropane at different concentrations: 2 M, 1M and 0.5 M from the graph shown in fig 7.2, the results obtained are tabulated below.

3. Rate law and rate constant:

We have just learnt that, the rate of the reaction depends upon the concentration of the reactant. Now let us understand how the reaction rate is related to concentration by considering the following general reaction.

xA + yB → products

The rate law for the above reaction is generally expressed as

Rate = k [A]^m [B]ⁿ

Where k is proportionality constant called the rate constant. The values of m and n represent the reaction order with respect to A and B respectively. The overall order of the reaction is given by (m+n). The values of the exponents (m and n) in the rate law must be determined by experiment. They cannot be deduced from the Stoichiometry of the reaction. For example, consider the isomerisation of cyclopropane, that we discussed earlier.

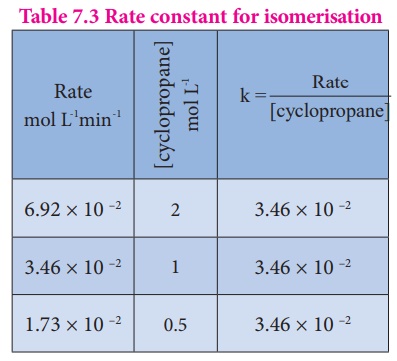
The results shown in table 7.2 indicate that if the concentration of cyclopropane is reduced to half, the rate also reduced to half. It means that the rate depends upon [cyclopropane] raised to the first power

i.e., Rate = k[cyclopropane]¹

Rate /[cyclopropane] = k

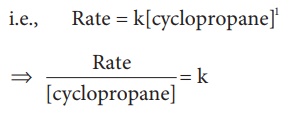
Rate constant for isomerisation

Let us consider an another example, the oxidation of nitric oxide (NO)

2NO(g) + O₂ (g ) 2NO₂ (g)

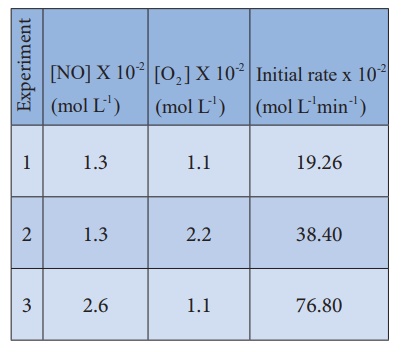
Series of experiments are conducted by keeping the concentration of one of the reactants constant and the changing the concentration of the others.

Rate = k [NO]^m[O₂]ⁿ

For experiment 1, the rate law is

Rate₁ = k [NO]^m[O₂]ⁿ

19.26 X10^-2 = k [1.3] ^m[1.1]ⁿ ...(1)

Similarly for experiment 2

Rate₂ = k [NO]^m [O₂ ]ⁿ

38.40 X10^-2 = k [1.3] ^m[2.2]ⁿ ...(2)

For experiment 3

Therefore the reaction is first order with respect to O₂

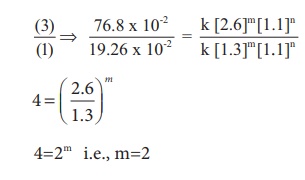
Therefore the reaction is second order with respect to NO

The rate law is Rate₁ = k [NO]²[O₂ ]¹

The overall order of the reaction = (2 + 1) = 3

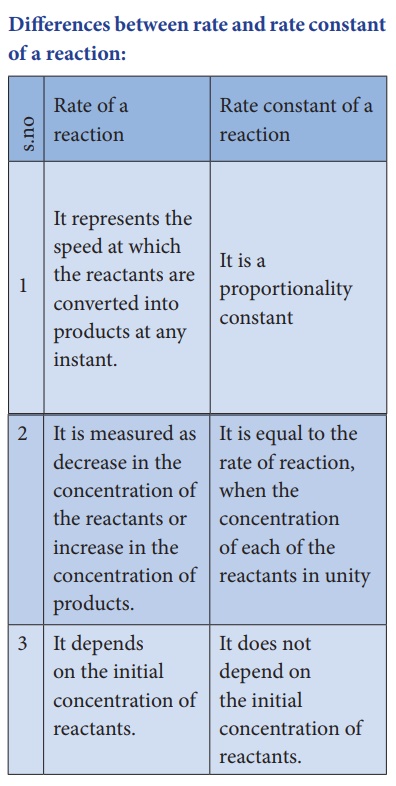
Differences between rate and rate constant of a reaction: