Arrhenius equation - The effect of temperature on reaction rate

Arrhenius equation - The effect of temperature on reaction rate

Generally, the rate of a reaction increase with increasing temperature. However, there are very few exceptions. The magnitude of this increase in rate is different for different reactions. As a rough rule, for many reactions near room temperature, reaction rate tends to double when the temperature is increased by 10ºC .

A large number of reactions are known which do not take place at room temperature but occur readily at higher temperatures. Example: Reaction between H₂ and O₂ to form H₂O takes place only when an electric spark is passed.

Arrhenius suggested that the rates of most reactions vary with temperature in such a way that the rate constant is directly proportional to e^-(E0/RT) and he proposed a relation between the rate constant and temperature.

Where A the frequency factor,

R the gas constant,

E_a the activation energy of the reaction and,

T the absolute temperature (in K)

The frequency factor (A) is related to the frequency of collisions (number of collisions per second) between the reactant molecules. The factor A does not vary significantly with temperature and hence it may be taken as a constant.

E_a is the activation energy of the reaction, which Arrhenius considered as the minimum energy that a molecule must have to posses to react.

Taking logarithm on both side of the equation (1)

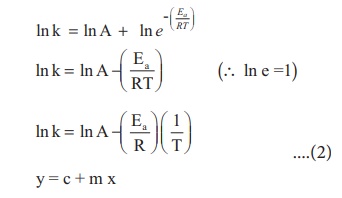
The above equation is of the form of a straight line y = mx + c.

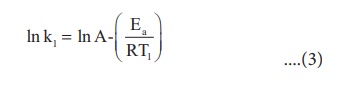
A plot of ln k Vs 1/T gives a straight line with a negative slope – E_a/R. If the rate constant for a reaction at two different temperatures is known, we can calculate the activation energy as follows.

At temperature T = T₁ ; the rate constant k = k₁

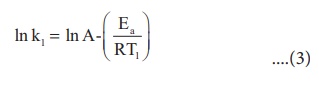
At temperature T = T₂ ; the rate constant k = k₂

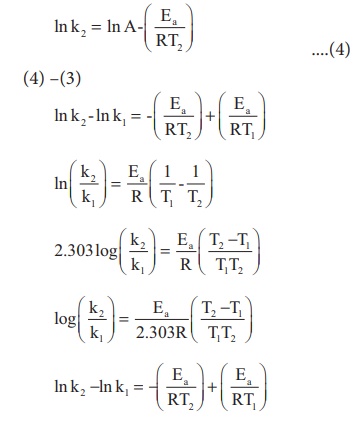
This equation can be used to calculate from rate constants k₁ and k₂ at temperatures T₁ and T_{2 .}

Example 7

The rate constant of a reaction at 400 and 200K are 0.04 and 0.02 s-1 respectively. Calculate the value of activation energy.

Solution

According to Arrhenius equation

Ea = 2305 J mol−1

Example 8

Rate constant k of a reaction varies with temperature T according to the following Arrhenius equation

Where Ea is the activation energy. When a graph is plotted for log k Vs 1/T a straight line with a slope of - 4000K is obtained. Calculate the activation energy

Solution

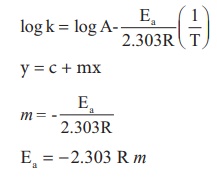
E_a = − 2.303 R m

E_a = − 2.303 x 8.314 J K⁻¹ mol⁻¹ x (− 4000K )

E_a = 76,589J mol⁻¹

E_a = 76.589 kJ mol⁻¹

Evaluate yourself

For a first order reaction the rate constant at 500K is 8 X 10⁻⁴ s⁻¹ . Calculate the frequency factor, if the energy of activation for the reaction is 190 kJ mol^-1 .