Boolean Algebra

BOOLEAN ALGEBRA

Boolean algebra is an algebraic structure defined by a set of elements, B, together with two binary operators, + and., provider that the following postulates are satisfied.

T1: Commutative Law

(a)A+B = B+A

(b)                        A B = BA

T2: Associative Law

(a) (A+B) +C = A+ (B+C)

(b) (A B) C = A (B C)

T3: Distributive Law

(a)  A (B +C) = A B + AC

(b) A + (B C) = (A +B) (A+C)

T4: Identity Law

(a)  A+A =A

(b) A A =A

T5: Negative Law

(a)  (A’) =A’

(b) (A’’) = A

T6: Redundant Law

(a)  A+AB=A

(b) A (A +B) =A

T7: Null Law

(a)0 + A = A

(b) 1 A = A

(c) 1 + A = 1

(d) 0 A = 0

T8: Double Negation Law

(a)  A’ +A=1

(b) A’ A=0

T9: Absorption Law

(a)  A+A’B =A+B

(b) A (A’ + B) =AB

T10: De Morgan's Theorem

(a)  (A+B)’ = A’ B’

(b) (AB)’ = A’+B’

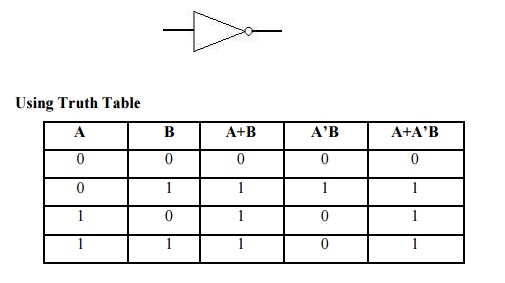
Example 1:

Using theorems,

A + A’ B = A l + A’ B

= A (l + B) + A’B

=A + AB + A’B

=A + B (A + A’)

= A + B

Using Truth Table

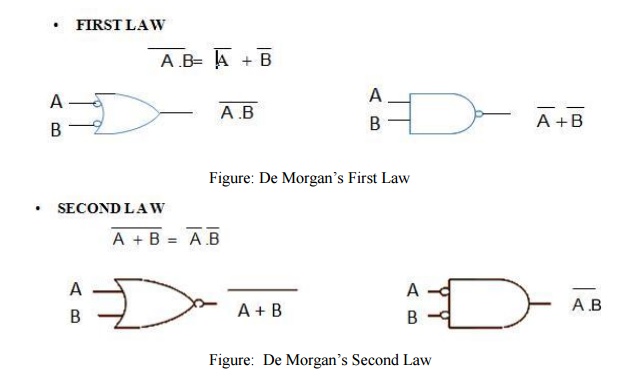
1 Verification Of De Morgan's Theorems:

•        De Morgan's First Theorem states:

The complement of a product of variables is equal to the sum of the complements of the individual variables

•        De Morgan's Second Theorem states:

The complement of sum of variables is equal to the product of the complements of the dividable variables