Chapter: Basic Electrical and electronics : Digital Electronics
Binary Number System
BINARY
NUMBER SYSTEM
Introduction
The number system that you
are familiar with, that you use every day, is the decimal number system, also
commonly referred to as the base-10 system. When you perform computations such
as 3 + 2 = 5, or 21 – 7 = 14, you are using the decimal number system. This
system, which you likely learned in first or second grade, is ingrained into
your subconscious; it’s the natural way that you think about numbers. Evidence
exists that Egyptians were using a decimal number system five thousand years
ago. The Roman numeral system, predominant for hundreds of years, was also a
decimal number system (though organized differently from the Arabic base-10
number system that we are most familiar with). Indeed, base-10 systems, in one
form or another, have been the most widely used number systems ever since
civilization started counting.
In dealing with the inner
workings of a computer, though, you are going to have to learn to think in a
different number system, the binary number system, also referred to as the
base-2 system.
Consider a child counting a
pile of pennies. He would begin: “One, two, three, …, eight, nine.” Upon
reaching nine, the next penny counted makes the total one single group of ten
pennies. He then keeps counting: “One group of ten pennies… two groups of ten
pennies… three groups of ten pennies … eight groups of ten pennies … nine
groups of ten pennies…” Upon reaching nine groups of ten pennies plus nine
additional pennies, the next penny counted makes the total thus far: one single
group of one hundred pennies. Upon completing the task, the child might find
that he has three groups of one hundred pennies, five groups of ten pennies,
and two pennies left over: 352 pennies.
More formally, the base-10
system is a positional system, where the rightmost digit is the ones position
(the number of ones), the next digit to the left is the tens position (the
number of groups of 10), the next digit to the left is the hundreds position
(the number of groups of 100), and so forth. The base-10 number system has 10
distinct symbols, or digits (0, 1, 2, 3,…8, 9). In decimal notation, we write a
number as a string of symbols, where each symbol is one of these ten digits,
and to interpret a decimal number, we multiply each digit by the power of 10
associated with that digit’s position.
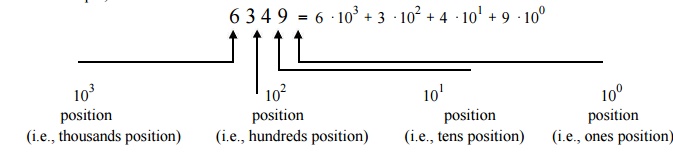
For
example, consider the decimal number: 6349. This number is:
Consider: Computers are built from transistors, and an individual
transistor can only be ON or OFF (two options). Similarly, data storage devices
can be optical or magnetic. Optical storage devices store data in a specific
location by controlling whether light is reflected off that location or is not
reflected off that location (two options). Likewise, magnetic storage devices
store data in a specific location by magnetizing the particles in that location
with a specific orientation. We can have the north magnetic pole pointing in
one direction, or the opposite direction (two options).
Computers can most readily use two symbols, and therefore a base-2
system, or binary number system, is most appropriate. The base-10 number system
has 10 distinct symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. The base-2 system has
exactly two symbols: 0 and 1. The base-10 symbols are termed digits. The base-2
symbols are termed binary digits, or bits for short. All base-10 numbers are
built as strings of digits (such as 6349). All binary numbers are built as
strings of bits (such as 1101). Just as we would say that the decimal number
12890 has five digits, we would say that the binary number 11001 is a five-bit
number.
2 The Binary Number System
Consider again the example of a child counting
a pile of pennies, but this time in binary.
He would
begin with the first penny: “1.” The next penny counted makes the total one
single group of two pennies. What number is this?
When the base-10 child reached nine (the highest symbol in his
scheme), the next penny gave him “one group of ten”, denoted as 10, where the
“1” indicated one collection of ten.
Similarly,
when the base-2 child reaches one (the highest symbol in his scheme), the next
penny gives him “one group of two”, denoted as 10, where the “1” indicates one
collection of two.
Back to the base-2 child: The next penny makes one group of two
pennies and one additional penny: “11.” The next penny added makes two groups
of two, which is one group of 4: “100.” The “1” here indicates a collection of
two groups of two, just as the “1” in the base-10 number 100 indicates ten groups
of ten.
Upon completing the counting task, base -2 child might find that he
has one group of four pennies, no groups of two pennies, and one penny left
over: 101 pennies. The child counting the same pile of pennies in base-10 would
conclude that there were 5 pennies. So, 5 in base-10 is equivalent to 101 in base-2. To avoid confusion when the base in
use if not clear from the context, or when using multiple bases in a single
expression, we append a subscript to the number to indicate the base, and write:
510 =1012
Just as with decimal notation, we write a binary number as a string
of symbols, but now each symbol is a 0 or a 1. To interpret a binary number, we multiply
each digit by the power of 2 associated with that digit’s position.
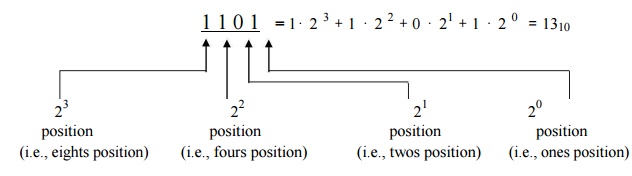
For example, consider the binary number 1101. This number is:
Since binary numbers can only contain the two symbols 0 and 1,
numbers such as 25 and 1114000 cannot be binary numbers.
We say that all data in a computer is stored in binary—that is, as
1’s and 0’s. It is important to keep in mind that values of 0 and 1 are logical
values, not the values of a physical quantity, such as a voltage. The actual
physical binary values used to store data internally within a computer might
be, for instance, 5 volts and 0 volts, or perhaps 3.3 volts and 0.3 volts or
perhaps reflection and no reflection. The two values that are used to
physically store data can differ within different portions of the same
computer. All that really matters is that there are two different symbols, so
we will always refer to them as 0 and 1.
A string of eight bits (such as 11000110) is termed a byte. A
collection of four bits (such as 1011) is smaller than a byte, and is hence
termed a nibble. (This is the sort of nerd-humor for which engineers are
famous.)
The idea
of describing numbers using a positional system, as we have illustrated for
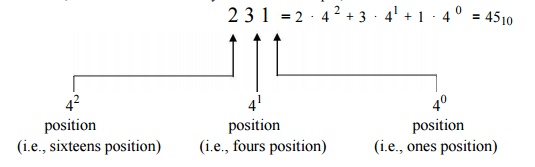
base-10 and base-2, can be extended to any base. For example, the base-4 number
231 is:
3 Converting Between Binary Numbers and Decimal
Numbers
We
humans about numbers using the decimal number system, whereas computers use the
binary number system. We need to be able to readily shift between the binary
and decimal number representations.
Converting
a Binary Number to a Decimal Number
To
convert a binary number to a decimal number, we simply write the binary number
as a sum of powers of 2. For example, to convert the binary number 1011 to a decimal number, we note that the
rightmost position is the ones position and the bit value in this position is a
1. So, this rightmost bit has the decimal value of 1⋅20 . The next position to the left
is the twos position, and the bit value in this position is also a 1. So, this next bit has the decimal value of 1⋅ 21 . The next position to the left
is the fours position, and the bit value in this position is a 0. The leftmost
position is the eights position, and the bit value in this position is a 1. So, this leftmost bit has the decimal value
of 1⋅23 . Thus:
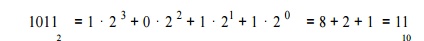
1. The binary number 110110 as a decimal number. Solution:
For example, to convert the binary number 10101 to decimal, we
annotate the position values below the bit values:

Then we add the position values for those positions that have a bit
value of 1: 16 + 4 + 1 = 21. Thus
101012 = 2110
You
should “memorize” the binary representations of the decimal digits 0 through 15
shown below.
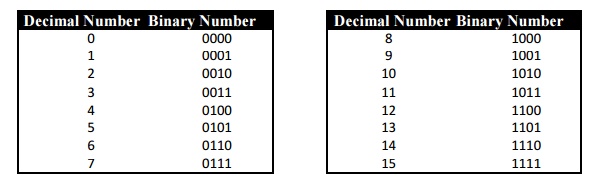
You may be wondering about the leading zeros in the table above.
For example, the decimal number 5 is represented in the table as the binary
number 0101. We could have represented the binary equivalent of 5 as 101,
00101, 0000000101, or with any other number of leading zeros. All answers are
correct.
Sometimes,
though, you will be given the size of a storage location. When you are given
the size of the storage location, include the leading zeros to show all bits in
the storage location. For example, if told to represent decimal 5 as an 8-bit
binary number, your answer should be 00000101.
Converting
a Decimal Number to a Binary Number: Method 2
The second method of converting a decimal number to a binary number
entails repeatedly dividing the decimal number by 2, keeping track of the
remainder at each step. To convert the decimal number x to binary:
Step 1. Divide x by 2 to obtain a quotient and remainder. The remainder will be 0
or 1.
Step 2. If the quotient is
zero, you are finished: Proceed to Step 3. Otherwise, go back to Step 1,
assigning x to be the value of the
most-recent quotient from Step 1.
Step 3. The sequence of remainders forms the
binary representation of the number.
4 Hexadecimal Numbers
In addition to binary, another number base that is commonly used in
digital systems is base 16. This number system is called hexadecimal, and each
digit position represents a power of 16. For any number base greater than ten,
a problem occurs because there are more than ten symbols needed to represent
the numerals for that number base. It is customary in these cases to use the
ten decimal numerals followed by the letters of the alphabet beginning with A
to provide the needed numerals. Since the hexadecimal system is base 16, there
are sixteen numerals required. The following are the hexadecimal numerals:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
The
following are some examples of hexadecimal numbers:
1016 4716 3FA16 A03F16
The reason for the common use of hexadecimal numbers is the
relationship between the numbers 2 and 16. Sixteen is a power of 2 (16 = 24).
Because of this relationship, four digits in a binary number can be represented
with a single hexadecimal digit. This makes conversion between binary and
hexadecimal numbers very easy, and hexadecimal can be used to write large
binary numbers with much fewer digits. When working with large digital systems,
such as computers, it is common to find binary numbers with 8, 16 and even 32
digits. Writing a 16 or 32 bit binary number would be quite tedious and error
prone. By using hexadecimal, the numbers can be written with fewer digits and much
less likelihood of error.
To convert a binary number to hexadecimal, divide it into groups of four digits starting with the rightmost digit. If the number of digits isn’t a multiple of 4, prefix the number with 0’s so that each group contains 4 digits. For each four digit group, convert the 4 bit binary number into an equivalent hexadecimal digit. (See the Binary, BCD, and Hexadecimal Number Tables at the end of this document for the correspondence between 4 bit binary patterns and hexadecimal digits)
2. Convert the binary number 10110101 to a hexadecimal
number

To convert a hexadecimal number to a binary number, convert each
hexadecimal digit into a group of 4 binary digits.
4. Convert the hex number 374F into binary
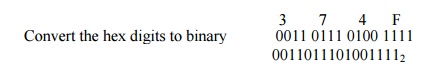
There are several ways in common use to specify that a given number
is in hexadecimal representation rather than some other radix. In cases where
the context makes it absolutely clear that numbers are represented in
hexadecimal, no indicator is used. In much written material where the context
doesn’t make it clear what the radix is, the numeric subscript 16 following the
hexadecimal number is used. In most programming languages, this method isn’t
really feasible, so there are several conventions used depending on the
language. In the C and C++ languages, hexadecimal constants are represented
with a ‘0x’ preceding the number, as in: 0x317F, or 0x1234, or 0xAF. In
assembler programming languages that follow the Intel style, a hexadecimal
constant begins with a numeric character (so that the assembler can distinguish
it from a variable name), a leading ‘0’ being used if necessary. The letter ‘h’
is then suffixed onto the number to inform the assembler that it is a
hexadecimal constant. In Intel style assembler format: 371Fh and
0FABCh
are valid hexadecimal constants. Note that: A37h isn’t a valid hexadecimal
constant. It doesn’t begin with a numeric character, and so will be taken by
the assembler as a variable name. In assembler programming languages that follow
the Motorola style, hexadecimal constants begin with a ‘$’ character. So in
this case: $371F or $FABC or $01 are valid hexadecimal constants.
5 Binary Coded Decimal Numbers
Another number system that is encountered occasionally is Binary
Coded Decimal. In this system, numbers are represented in a decimal form,
however each decimal digit is encoded using a four bit binary number.
The
decimal number 136 would be represented in BCD as follows: 136 = 0001 0011 0110
1 3 6
Conversion of numbers between decimal and BCD is quite simple. To
convert from decimal to BCD, simply write down the four bit binary pattern for
each decimal digit. To convert from BCD to decimal, divide the number into
groups of 4 bits and write down the corresponding decimal digit for each 4 bit
group.
There are a couple of variations on the BCD representation, namely
packed and unpacked. An unpacked BCD number has only a single decimal digit
stored in each data byte. In this case, the decimal digit will be in the low
four bits and the upper 4 bits of the byte will be 0. In the packed BCD
representation, two decimal digits are placed in each byte. Generally, the high
order bits of the data byte contain the more significant decimal digit.
6. The following is a 16 bit number encoded in packed
BCD format:
01010110 10010011
This is converted to a
decimal number as follows: 0101 0110 1001 0011
5 6 9 3 The value is 5693
decimal
7. The same number in unpacked BCD (requires 32
bits)
00000101 00000110 00001001 00000011
5 6 9 3
The use of BCD to represent numbers isn’t as common as binary in
most computer systems, as it is not as space efficient. In packed BCD, only 10
of the 16 possible bit patterns in each 4 bit unit are used. In unpacked BCD,
only 10 of the 256 possible bit patterns in each byte are used. A 16 bit
quantity can represent the range 0-65535 in binary, 0-9999 in packed BCD and
only 0-99 in unpacked BCD.
Fixed Precision and Overflow
we haven’t considered the maximum size of the number. We have
assumed that as many bits are available as needed to represent the number. In
most computer systems, this isn’t the case. Numbers in computers are typically
represented using a fixed number of bits. These sizes are typically 8 bits, 16
bits, 32 bits, 64 bits and 80 bits. These sizes are generally a multiple of 8,
as most computer memories are organized on an 8 bit byte basis. Numbers in
which a specific number of bits are used to represent the value are called
fixed precision numbers. When a specific number of bits are used to represent a
number, that determines the range of possible values that can be represented.
For example, there are 256 possible combinations of 8 bits, therefore an 8 bit
number can represent 256 distinct numeric values and the range is typically
considered to be 0-255. Any number larger than 255 can’t be represented using 8
bits. Similarly,
16 bits
allows a range of 0-65535.
When
fixed precision numbers are used, (as they are in virtually all computer
calculations) the concept of overflow must be considered. An overflow occurs
when the result of a calculation can’t be represented with the number of bits
available. For example when adding the two eight bit quantities: 150 + 170, the
result is 320. This is outside the range 0-255, and so the result can’t be
represented using 8 bits. The result has overflowed the available range. When
overflow occurs, the low order bits of the result will remain valid, but the
high order bits will be lost. This results in a value that is significantly
smaller than the correct result.
When doing fixed precision arithmetic (which all computer
arithmetic involves) it is necessary to be conscious of the possibility of
overflow in the calculations.
Signed and Unsigned Numbers.
we have only considered positive values for binary numbers. When a
fixed precision binary number is used to hold only positive values, it is said
to be unsigned. In this case, the range of positive values that can be
represented is 0 -- 2n-1, where n is the number of bits used. It is
also possible to represent signed (negative as well as positive) numbers in
binary. In this case, part of the total range of values is used to represent
positive values, and the rest of the range is used to represent negative
values.
There are several ways that signed numbers can be represented in
binary, but the most common representation used today is called two’s
complement. The term two’s complement is somewhat ambiguous, in that it is used
in two different ways. First, as a representation, two’s complement is a way of
interpreting and assigning meaning to a bit pattern contained in a fixed
precision binary quantity. Second, the term two’s complement is also used to
refer to an operation that can be performed on the bits of a binary quantity.
As an operation, the two’s complement of a number is formed by inverting all of
the bits and adding 1. In a binary number being interpreted using the two’s
complement representation, the high order bit of the number indicates the sign.
If the sign bit is 0, the number is positive, and if the sign bit is 1, the
number is negative. For positive numbers, the rest of the bits hold the true
magnitude of the number. For negative numbers, the lower order bits hold the
complement (or bitwise inverse) of the magnitude of the number. It is important
to note that two’s complement representation can only be applied to fixed
precision quantities, that is, quantities where there are a set number of bits.
Two’s complement representation is used because it reduces the
complexity of the hardware in the arithmetic-logic unit of a computer’s CPU.
Using a two’s complement representation, all of the arithmetic operations can
be performed by the same hardware whether the numbers are considered to be
unsigned or signed. The bit operations performed are identical, the difference comes
from the interpretation of the bits. The interpretation of the value will be
different depending on whether the value is considered to be unsigned or
signed.
8. Find the 2’s complement of the following
8 bit number

The 2’s complement of 00101001 is 11010111
9. Find the 2’s complement of the following 8 bit number 10110101

The 2’s complement of 10110101 is 01001011
The
counting sequence for an eight bit binary value using 2’s complement
representation appears as follows:
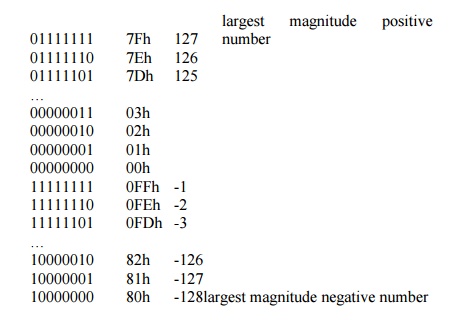
Counting up from 0, when 127 is reached, the next binary pattern in
the sequence corresponds to -128. The values jump from the greatest positive
number to the greatest negative number, but that the sequence is as expected after
that. (i.e. adding 1 to –128 yields –127, and so on.). When the count has
progressed to 0FFh (or the largest unsigned magnitude possible) the count wraps
around to 0. (i.e. adding 1 to –1 yields 0).
ASCII Character Encoding
The name
ASCII is an acronym for: American Standard Code for Information Interchange. It
is a character encoding standard developed several decades ago to provide a
standard way for digital machines to encode characters. The ASCII code provides
a mechanism for encoding alphabetic characters, numeric digits, and punctuation
marks for use in representing text and numbers written using the Roman
alphabet. As originally designed, it was a seven bit code. The seven bits allow
the representation of 128 unique characters. All of the alphabet, numeric
digits and standard English punctuation marks are encoded. The ASCII standard
was later extended to an eight bit code (which allows 256 unique code patterns)
and various additional symbols were added, including characters with
diacritical marks (such as accents) used in European languages, which don’t
appear in English. There are also numerous non-standard extensions to ASCII
giving different encoding for the upper 128 character codes than the standard.
For example, The character set encoded into the display card for the original
IBM PC had a non-standard encoding for the upper character set. This is a
non-standard extension that is in very wide spread use, and could be considered
a standard in itself.
The numeric digits, 0-9, are encoded in
sequence starting at 30h The upper case alphabetic characters are sequential
beginning at 41h The lower case alphabetic characters are sequential beginning
at 61h
The first 32 characters (codes 0-1Fh) and 7Fh
are control characters. They do not have a standard symbol (glyph) associated
with them. They are used for carriage control, and protocol purposes. They
include 0Dh (CR or carriage return), 0Ah (LF or line feed), 0Ch (FF or form
feed), 08h (BS or backspace).
Most keyboards generate the control characters
by holding down a control key (CTRL) and simultaneously pressing an alphabetic
character key. The control code will have the same value as the lower five bits
of the alphabetic key pressed. So, for example, the control character 0Dh is
carriage return. It can be generated by pressing CTRL-M. To get the full 32
control characters a few at the upper end of the range are generated by
pressing CTRL and a punctuation key in combination. For example, the ESC
(escape) character is generated by pressing CTRL-[ (left square bracket).
ASCII code chart that the uppercase letters start at 41h and that
the lower case letters begin at 61h. In each case, the rest of the letters are
consecutive and in alphabetic order. The difference between 41h and 61h is 20h.
Therefore the conversion between upper and lower case involves either adding or
subtracting 20h to the character code. To convert a lower case letter to upper
case, subtract 20h, and conversely to convert upper case to lower case, add
20h. It is important to note that you need to first ensure that you do in fact
have an alphabetic character before performing the addition or subtraction.
Ordinarily, a check should be made that the character is in the range 41h–5Ah
for upper case or 61h-7Ah for lower case.
Conversion Between ASCII and BCD
ASCII
code chart that the numeric characters are in the range 30h-39h. Conversion
between an ASCII encoded digit and an unpacked BCD digit can be accomplished by
adding or subtracting 30h. Subtract 30h from an ASCII digit to get BCD, or add
30h to a BCD digit to get ASCII. Again, as with upper and lower case conversion
for alphabetic characters, it is necessary to ensure that the character is in
fact a numeric digit before performing the subtraction. The digit characters
are in the range 30h-39h.
Related Topics