Writing a Grammar

Writing a Grammar

1 Lexical Versus Syntactic Analysis

2 Eliminating Ambiguity

3 Elimination of Left Recursion

4 Left Factoring

5 Non-Context-Free Language Constructs

6 Exercises for Section 4.3

Grammars are capable of describing most, but not all, of the syntax of pro-gramming languages. For instance, the requirement that identifiers be declared before they are used, cannot be described by a context-free grammar. Therefore, the sequences of tokens accepted by a parser form a superset of the program-ming language; subsequent phases of the compiler must analyze the output of the parser to ensure compliance with rules that are not checked by the parser.

This section begins with a discussion of how to divide work between a lexical analyzer and a parser. We then consider several transformations that could be applied to get a grammar more suitable for parsing. One technique can elim-inate ambiguity in the grammar, and other techniques — left-recursion elimi-nation and left factoring — are useful for rewriting grammars so they become suitable for top-down parsing. We conclude this section by considering some programming language constructs that cannot be described by any grammar.

1. Lexical Versus Syntactic Analysis

As we observed in Section 4.2.7, everything that can be described by a regular expression can also be described by a grammar. We may therefore reasonably ask: "Why use regular expressions to define the lexical syntax of a language?" There are several reasons.

            Separating the syntactic structure of a language into lexical and non-lexical parts provides a convenient way of modularizing the front end of

a compiler into two manageable-sized components.

            The lexical rules of a language are frequently quite simple, and to describe them we do not need a notation as powerful as grammars.

            Regular expressions generally provide a more concise and easier-to-under-stand notation for tokens than grammars.

            More efficient lexical analyzers can be constructed automatically from regular expressions than from arbitrary grammars.

There are no firm guidelines as to what to put into the lexical rules, as op-posed to the syntactic rules. Regular expressions are most useful for describing the structure of constructs such as identifiers, constants, keywords, and white space. Grammars, on the other hand, are most useful for describing nested structures such as balanced parentheses, matching begin-end's, corresponding if-then-else's, and so on. These nested structures cannot be described by regular expressions.

2. Eliminating Ambiguity

Sometimes an ambiguous grammar can be rewritten to eliminate the ambiguity. As an example, we shall eliminate the ambiguity from the following "dangling-else" grammar:

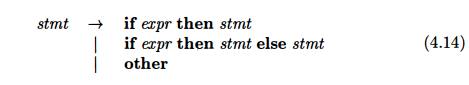
Here "other" stands for any other statement. According to this grammar, the compound conditional statement

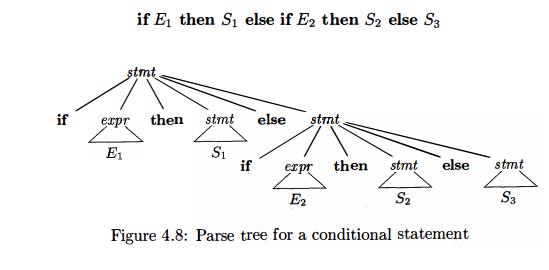
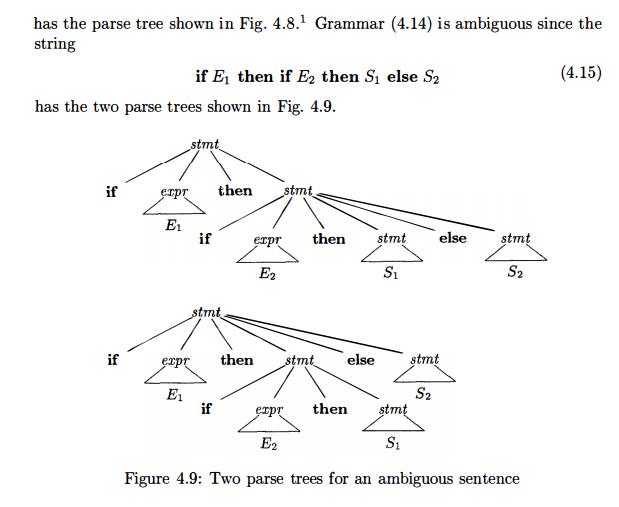
In all programming languages with conditional statements of this form, the first parse tree is preferred. The general rule is, "Match each else with the closest unmatched then . " ² This disambiguating rule can theoretically be in-corporated directly into a grammar, but in practice it is rarely built into the productions.

Example 4.16 : We can rewrite the dangling-else grammar (4.14) as the fol-lowing unambiguous grammar. The idea is that a statement appearing between a t h e n and an else must be "matched"; that is, the interior statement must not end with an unmatched or open then . A matched statement is either an if-then-else statement containing no open statements or it is any other kind of unconditional statement. Thus, we may use the grammar in Fig. 4.10. This grammar generates the same strings as the dangling-else grammar (4.14), but it allows only one parsing for string (4.15); namely, the one that associates each else with the closest previous unmatched then . •

3. Elimination of Left Recursion

A grammar is left recursive if it has a nonterminal A such that there is a derivation A 4 Aa for some string a. Top-down parsing methods cannot handle left-recursive grammars, so a transformation is needed to eliminate left recursion. In Section 2.4.5, we discussed immediate left recursion, where there is a production of the form A ->• Aa. Here, we study the general case. In Section 2.4.5, we showed how the left-recursive pair of productions A -»• Aa | b could be replaced by the non-left-recursive productions:

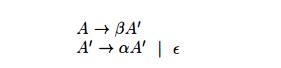
without changing the strings derivable from A. This rule by itself suffices for many grammars.

Example 4.17 : The non-left-recursive expression grammar (4.2), repeated here,

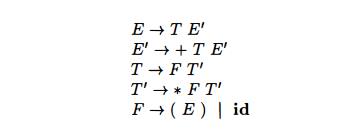
is obtained by eliminating immediate left recursion from the expression gram-mar (4.1). The left-recursive pair of productions E -» E + T | T are replaced by E -> T E' and E' -»• + T E' | e. The new productions for T and T' are obtained similarly by eliminating immediate left recursion. •

Immediate left recursion can be eliminated by the following technique, which works for any number of A-productions. First, group the productions as

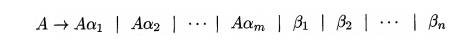
where no bi begins with an A.  Then, replace the A-productions by

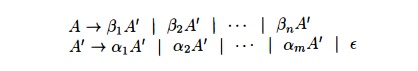
This procedure eliminates all left recursion from the A and A' pro-ductions (provided no is e), but it does not eliminate left recursion involving derivations of two or more steps. For example, consider the grammar

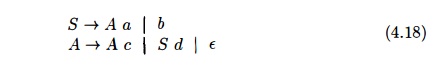
The nonterminal S  is left  recursive because  S =>Aa=> Sda,  but  it  is  not immediately left recursive.

Algorithm 4.19, below, systematically eliminates left recursion from a gram-mar. It is guaranteed to work if the grammar has no cycles (derivations of the form A=>* A) or e-productions (productions of the form A —> e). Cycles can be eliminated systematically from a grammar, as can e-productions (see Exercises 4.4.6 and 4.4.7).

Algorithm 4. 1 9 :  Eliminating left recursion.

INPUT : Grammar G with no cycles or e-productions.

OUTPUT : An equivalent grammar with no left recursion.

METHOD : Apply the algorithm in Fig. 4.11 to G. Note that the resulting non-left-recursive grammar may have e-productions.

Figure 4.11:  Algorithm to eliminate left recursion from a grammar

The procedure in Fig. 4.11 works as follows. In the first iteration for % = 1, the outer for-loop of lines (2) through (7) eliminates any immediate left recursion among A1-productions. Any remaining A1 productions of the form A1 —> A1a must therefore have / > 1. After the i — 1st iteration of the outer for-loop, all nonterminals Ak, where k < i, are "cleaned"; that is, any production Ak —> Aia, must have I > k. As a result, on the ith. iteration, the inner loop of lines (3) through (5) progressively raises the lower limit in any production Ai -> A ma, until we have m > i. Then, eliminating immediate left recursion for the Ai productions at line (6) forces m to be greater than i.

Example 4.20 :  Let us apply Algorithm 4.19 to the grammar (4.18).  Technically, the algorithm is not guaranteed to work, because of the e-production, but in this case, the production A -» e turns out to be harmless.

We order the nonterminals S, A. There is no immediate left recursion among the 5-productions, so nothing happens during the outer loop for i = 1. For i = 2, we substitute for S in A —> S d to obtain the following ^.-productions.

A-> Ac | Aa d | b d | e

Eliminating the immediate left recursion among these ^-productions yields the following grammar.

S->Aa |  b 

A->bdA'  | A' 

A'-> cA'  | ad  A' | e

4. Left Factoring

Left factoring is a grammar transformation that is useful for producing a gram-mar suitable for predictive, or top-down, parsing. When the choice between two alternative ^-productions is not clear, we may be able to rewrite the pro-ductions to defer the decision until enough of the input has been seen that we can make the right choice.

For example, if we have the two productions

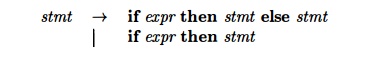
on seeing the input if, we cannot immediately tell which production to choose to expand stmt. In general, if A ->• a b1 | a b2 are two A-productions, and the input begins with a nonempty string derived from a, we do not know whether to expand A to a b1 or ab2 . However, we may defer the decision by expanding A to aA'. Then, after seeing the input derived from a, we expand A' to b1 or to b2. That is, left-factored, the original productions become

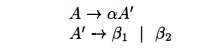
Algorithm 4.21 : Left factoring a grammar.

INPUT : Grammar G.

OUTPUT : An equivalent left-factored grammar.

Thus, we may expand 5 to iEtSS' on input i, and wait until i EtS has been seen to decide whether to expand S' to eS or to e. Of course, these grammars are both ambiguous, and on input e, it will not be clear which alternative for S' should be chosen. Example 4.33 discusses a way out of this dilemma. •

5. Non-Context-Free Language Constructs

A few syntactic constructs found in typical programming languages cannot be specified using grammars alone. Here, we consider two of these constructs, using simple abstract languages to illustrate the difficulties.

Example 4.25 : The language in this example abstracts the problem of checking that identifiers are declared before they are used in a program. The language consists of strings of the form wcw, where the first w represents the declaration of an identifier w, c represents an intervening program fragment, and the second w represents the use of the identifier.

The abstract language is L1 — {wcw 1 w is in (a|b)*} . L1 consists of all words composed of a repeated string of a's and 6's separated by c, such as aabcaab. While it is beyond the scope of this book to prove it, the non-context-freedom of Li directly implies the non-context-freedom of programming languages like C and Java, which require declaration of identifiers before their use and which allow identifiers of arbitrary length.

For this reason, a grammar for C or Java does not distinguish among identi-fiers that are different character strings. Instead, all identifiers are represented by a token such as id in the grammar. In a compiler for such a language, the semantic-analysis phase checks that identifiers are declared before they are used. •

Example 4.26 : The non-context-free language in this example abstracts the problem of checking that the number of formal parameters in the declaration of a function agrees with the number of actual parameters in a use of the function.

The language consists of strings of the form anbmcndm. (Recall an means a written n times.) Here an and bm could represent the formal-parameter lists of two functions declared to have n and m arguments, respectively, while cn and dm represent the actual-parameter lists in calls to these two functions.

The abstract language is L2 = {aⁿb^mcⁿd^m 1 n >= 1 and m >= 1}.  That is, L2 consists of strings in the language generated by the regular expression a*b*c*d* such that the number of a's and c's are equal and the number of 6's and d's are equal. This language is not context free.

Again, the typical syntax of function declarations and uses does not concern itself with counting the number of parameters. For example, a function call in C-like language might be specified by

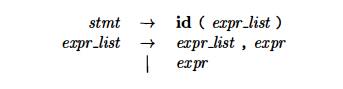
with suitable productions for expr.        Checking that the number of parameters in a call is correct is usually done during the semantic-analysis phase.

6. Exercises for Section 4.3

Exercise 4 . 3 . 1 : The following is a grammar for regular expressions over sym-bols a and b only, using + in place of | for union, to avoid conflict with the use of vertical bar as a metasymbol in grammars:

          Left factor this grammar.

          Does left factoring make the grammar suitable for top-down parsing?

          In addition to left factoring, eliminate left recursion from the original grammar.

          Is the resulting grammar suitable for top-down parsing?

Exercise 4 . 3 . 2:  Repeat Exercise 4.3.1 on the following grammars:

            The grammar of Exercise 4.2.1.

            The grammar of Exercise 4.2.2(a).

                     The grammar of Exercise 4.2.2(c).

                     The grammar of Exercise 4.2.2(e).

                      The grammar of Exercise 4.2.2(g).

      Exercise 4 . 3 . 3 : The following grammar is proposed to remove the "dangling-else ambiguity" discussed in Section 4.3.2:

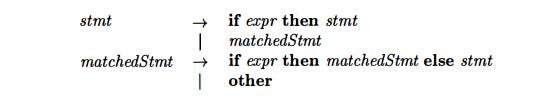
Show that this grammar is still ambiguous.