Top-Down Parsing

Top-Down Parsing

1 Recursive-Descent Parsing

2 FIRST and FOLLOW

3 LL(1) Grammars

4 Nonrecursive Predictive Parsing

5 Error Recovery in Predictive Parsing

6 Exercises for Section 4.4

Top-down parsing can be viewed as the problem of constructing a parse tree for the input string, starting from the root and creating the nodes of the parse tree in preorder (depth-first, as discussed in Section 2.3.4). Equivalently, top-down parsing can be viewed as finding a leftmost derivation for an input string.

E x a m p l e 4 . 2 7 : The sequence of parse trees in Fig. 4.12 for the input id+id*id is a top-down parse according to grammar (4.2), repeated here:

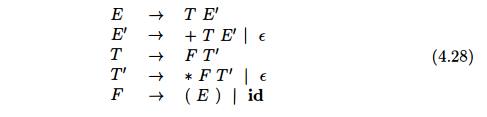
This sequence of trees corresponds to a leftmost derivation of the input.

At each step of a top-down parse, the key problem is that of determining the production to be applied for a nonterminal, say A. Once an A-production is chosen, the rest of the parsing process consists of "matching" the terminal symbols in the production body with the input string.

The section begins with a general form of top-down parsing, called recursive-descent parsing, which may require backtracking to find the correct A-produc-tion to be applied. Section 2.4.2 introduced predictive parsing, a special case of recursive-descent parsing, where no backtracking is required. Predictive parsing chooses the correct A-production by looking ahead at the input a fixed number of symbols, typically we may look only at one (that is, the next input symbol).

For example, consider the top-down parse in Fig. 4.12, which constructs a tree with two nodes labeled E'. At the first E' node (in preorder), the production E' —> +TE' is chosen; at the second E' node, the production E' —> e is chosen. A predictive parser can choose between E'-productions by looking at the next input symbol.

The class of grammars for which we can construct predictive parsers looking k symbols ahead in the input is sometimes called the LL(k) class. We discuss the LL(1) class in Section 4.4.3, but introduce certain computations, called FIRST and FOLLOW, in a preliminary Section 4.4.2. From the FIRST and FOLLOW sets for a grammar, we shall construct "predictive parsing tables," which make explicit the choice of production during top-down parsing. These sets are also useful during bottom-up parsing,

In Section 4.4.4 we give a nonrecursive parsing algorithm that maintains a stack explicitly, rather than implicitly via recursive calls. Finally, in Section 4.4.5 we discuss error recovery during top-down parsing.

1. Recursive-Descent Parsing

          void A{)  {         

          Choose an A-production, A X1X2   - • • Xk1

          for ( i = 1 to k ) {

          if ( X{ is a nonterminal )

                   call  procedure  XiQ;

          else   if ( Xi equals the current input symbol a )

          advance the input to the next symbol;

          else   /* an error has occurred */;

}

}

Figure 4.13:  A typical procedure for a nonterminal in a top-down parser

A recursive-descent parsing program consists of a set of procedures, one for each nonterminal. Execution begins with the procedure for the start symbol, which halts and announces success if its procedure body scans the entire input string. Pseudocode for a typical nonterminal appears in Fig. 4.13. Note that this pseudocode is nondeterministic, since it begins by choosing the A-production to apply in a manner that is not specified.

General recursive-descent may require backtracking; that is, it may require repeated scans over the input. However, backtracking is rarely needed to parse programming language constructs, so backtracking parsers are not seen fre-quently. Even for situations like natural language parsing, backtracking is not very efficient, and tabular methods such as the dynamic programming algo-rithm of Exercise 4.4.9 or the method of Earley (see the bibliographic notes) are preferred.

To allow backtracking, the code of Fig. 4.13 needs to be modified. First, we cannot choose a unique A-production at line (1), so we must try each of several productions in some order. Then, failure at line (7) is not ultimate failure, but suggests only that we need to return to line (1) and try another A-production. Only if there are no more A-productions to try do we declare that an input error has been found. In order to try another A-production, we need to be able to reset the input pointer to where it was when we first reached line (1). Thus, a local variable is needed to store this input pointer for future use.

E x a m p l e 4 . 2 9 :  Consider the grammar

S -> cAd

A -> a b | a

To construct a parse tree top-down for the input string w = cad, begin with a tree consisting of a single node labeled S, and the input pointer pointing to c, the first symbol ofw.S has only one production, so we use it to expand S and obtain the tree of Fig. 4.14(a). The leftmost leaf, labeled c, matches the first symbol of input w, so we advance the input pointer to a, the second symbol of w, and consider the next leaf, labeled A.

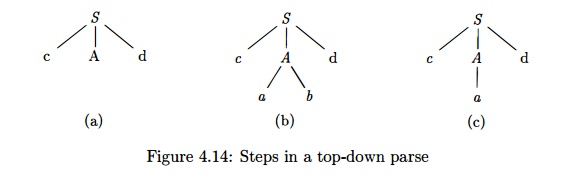
Now, we expand A using the first alternative A -> a b to obtain the tree of Fig. 4.14(b). We have a match for the second input symbol, a, so we advance the input pointer to d, the third input symbol, and compare d against the next leaf, labeled b. Since b does not match d, we report failure and go back to A to see whether there is another alternative for A that has not been tried, but that might produce a match.

In going back to A, we must reset the input pointer to position 2, the position it had when we first came to A, which means that the procedure for A must store the input pointer in a local variable.

The second alternative for A produces the tree of Fig.  4.14(c). The leaf a matches the second symbol of w  and the leaf d matches the third symbol. Since we have produced a parse tree for w,  we halt and announce successful completion of parsing.

A left-recursive grammar can cause a recursive-descent parser, even one with backtracking, to go into an infinite loop. That is, when we try to expand a nonterminal A, we may eventually find ourselves again trying to expand A without having consumed any input.

2. FIRST and FOLLOW

The construction of both top-down and bottom-up parsers is aided by two functions, FIRST and FOLLOW, associated with a grammar G. During top-down parsing, FIRST and FOLLOW allow us to choose which production to apply, based on the next input symbol. During panic-mode error recovery, sets of tokens produced by FOLLOW can be used as synchronizing tokens.

Example 4.30 : Consider again the non-left-recursive grammar (4.28). Then:

1. FIRST (F ) = FIRST(T ) = FIRST (E ) = {(,id} . To see why, note that the two productions for F have bodies that start with these two terminal symbols, id and the left parenthesis. T has only one production, and its body starts with F. Since F does not derive e, FIRST (T ) must be the same as FIRST (F). The same argument covers FIRST (E).

2. FIRST (E ' ) = {+, e}. The reason is that one of the two productions for E' has a body that begins with terminal +, and the other's body is e. Whenever a nonterminal derives e, we place e in FIRST for that nonterminal.

3. FIRST (T ' ) = {*,e}. The reasoning is analogous to that for FIRST (E ' ) -

4. FOLLOW ( E ) = FOLLOW ( E ' ) = {), $ } . Since E is the start symbol, FOLLOW ( E ) must contain $. The production body ( E ) explains why the right parenthesis is in FOLLOW ( E ) . For E', note that this nonterminal appears only at the ends of bodies of E-productions. Thus, FOLLOW ( E' ) must be the same as FOLLOW ( E ) .

5. FOLLOW ( T ) = FOLLOW ( T ' ) = { + , ) , $}. Notice that T appears in bodies only followed by E'. Thus, everything except e that is in FIRST (E ' ) must be in FOLLOW ( T ) ; that explains the symbol +. However, since FIRST (E ' ) contains e (i.e., E' 4* e), and E' is the entire string following T in the bodies of the E-productions, everything in FOLLOW ( E ) must also be in FOLLOW ( T ) . That explains the symbols $ and the right parenthesis. As for T", since it appears only at the ends of the T-productions, it must be that FOLLOW ( T ' ) = FOLLOW ( T ) .

6. FOLLOW ( F ) = { + , * , ) , $ } . The reasoning is analogous to that for T in point (5).

3. LL(1) Grammars

Predictive parsers, that is, recursive-descent parsers needing no backtracking, can be constructed for a class of grammars called LL(1). The first "L" in LL(1) stands for scanning the input from left to right, the second "L" for producing a leftmost derivation, and the " 1 " for using one input symbol of lookahead at each step to make parsing action decisions.

Transition Diagrams for Predictive Parsers

Transition diagrams are useful for visualizing predictive parsers. For exam-ple, the transition diagrams for nonterminals E and E' of grammar (4.28) appear in Fig. 4.16(a). To construct the transition diagram from a gram-mar, first eliminate left recursion and then left factor the grammar. Then, for each nonterminal A,

1. Create an initial and final (return) state.

2. For each production A -> X1X2 ......... Xk, create a path from the initial to the final state, with edges labeled X1,X2, ...... , If A -» e, the path is an edge labeled e.

Transition diagrams for predictive parsers differ from those for lexical analyzers. Parsers have one diagram for each nonterminal. The labels of edges can be tokens or nonterminals. A transition on a token (terminal)

means that we take that transition if that token is the next input symbol. A transition on a nonterminal A is a call of the procedure for A.

With an LL(1) grammar, the ambiguity of whether or not to take an e-edge can be resolved by making e-transitions the default choice.

Transition diagrams can be simplified, provided the sequence of gram-mar symbols along paths is preserved. We may also substitute the dia-gram for a nonterminal A in place of an edge labeled A. The diagrams in Fig. 4.16(a) and (b) are equivalent: if we trace paths from E to an accept-ing state and substitute for E', then, in both sets of diagrams, the grammar

symbols along the paths make up strings of the form T + T-1 --  h T.  The diagram in (b) can be obtained from (a) by transformations akin to those in Section 2.5.4, where we used tail-recursion removal and substitution of procedure bodies to optimize the procedure for a nonterminal.

The class of LL(1) grammars is rich enough to cover most programming constructs, although care is needed in writing a suitable grammar for the source language. For example, no left-recursive or ambiguous grammar can be LL(1).

A grammar G is LL(1) if and only if whenever A —> a | b sere two distinct productions of G, the following conditions hold:

1. For no terminal a do both a and b derive strings beginning with a.

2. At most one of a and b can derive the empty string.

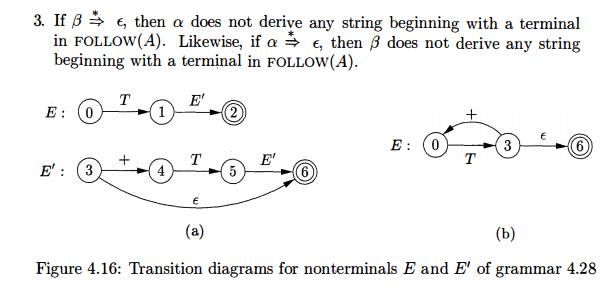
Figure 4.16:  Transition diagrams for nonterminals E and E' of grammar 4.28

The first two conditions are equivalent to the statement that FIRST (a) and FIRST(b) are disjoint sets. The third condition is equivalent to stating that if e is in FIRST(b), then FIRST (a) and FOLLOW(A) are disjoint sets, and likewise if e is in FIRST (a).

Predictive parsers can be constructed for LL(1) grammars since the proper production to apply for a nonterminal can be selected by looking only at the current input symbol. Flow-of-control constructs, with their distinguishing key-words, generally satisfy the LL(1) constraints. For instance, if we have the productions

then the keywords if, while, and the symbol { tell us which alternative is the only one that could possibly succeed if we are to find a statement.

The next algorithm collects the information from FIRST and FOLLOW sets into a predictive parsing table M[A,a], a two-dimensional array, where A is a nonterminal, and a is a terminal or the symbol $, the input endmarker. The algorithm is based on the following idea: the production A —> a is chosen if the next input symbol a is in FIRST (a) . The only complication occurs when a = e or, more generally, a =>* e. In this case, we should again choose A -» a, if the current input symbol is in FOLLOW(A), or if the $ on the input has been reached and $ is in FOLLOW (A).

Algorith m 4 . 3 1 :       Construction of a predictive parsing table.

INPUT :  Grammar G.

OUTPUT : Parsing table M.

METHOD : For each production A -> a of the grammar, do the following:

1. For each terminal a in FIRST(A), add A -4 a to M[A, a].

2.   If e is in F l R S T ( a ) , then for each terminal 6 in FOLLOW(A), add A -»• a to M[A,b]. If e is in FIRST (a) and $ is in FOLLOW(A), add A -4 a to M[A, $] as well.

If, after performing the above, there is no production at all in M[A, a], then set M[A, a] to e r r o r (which we normally represent by an empty entry in the table).

Example 4.32 : For the expression grammar (4.28), Algorithm 4.31 produces the parsing table in Fig. 4.17. Blanks are error entries; nonblanks indicate a production with which to expand a nonterminal.

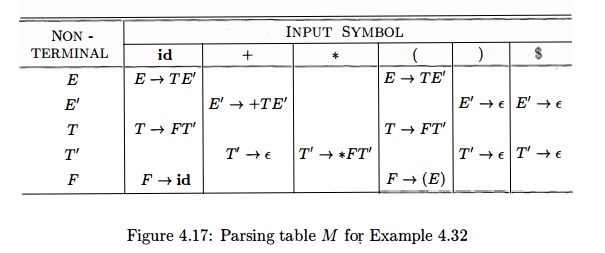
Consider production E -> T E ' . Since      

   F I R S T ( T E ' ) =  F I R S T ( T ) =  {(,id} 

this production is added to M[E,{]  and M[E, id].  Production E'  ->• + T F / is added  to  M[E',+] since  F I R S T ( + T E ' ) =  { + } . Since F O L L O W ^ ' ) =  { ) , $ } , production E' -+ e is added to M[E',)] and M[E', $].

Algorithm 4.31 can be applied to any grammar G to produce a parsing table M. For every LL(1) grammar, each parsing-table entry uniquely identifies a production or signals an error. For some grammars, however, M may have some entries that are multiply defined. For example, if G is left-recursive or ambiguous, then M will have at least one multiply defined entry. Although left-recursion elimination and left factoring are easy to do, there are some grammars for which no amount of alteration will produce an LL(1) grammar.

The language in the following example has no LL(1) grammar at all.

Example 4 . 3 3 : The following grammar, which abstracts the dangling-else problem, is repeated here from Example 4.22:

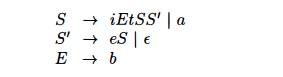
The parsing table for this grammar appears in Fig. 4.18. The entry for M[S', e) contains both S' —> eS and S' —> e.

The grammar is ambiguous and the ambiguity is manifested by a choice in what production to use when an e (else) is seen. We can resolve this ambiguity

by choosing S' -» eS. This choice corresponds to associating an else with the closest previous then . Note that the choice S' -> e would prevent e from ever being put on the stack or removed from the input, and is surely wrong. •

4. Nonrecursive Predictive Parsing

A nonrecursive predictive parser can be built by maintaining a stack explicitly, rather than implicitly via recursive calls. The parser mimics a leftmost derivation. If w is the input that has been matched so far, then the stack holds a sequence of grammar symbols a such that

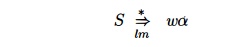
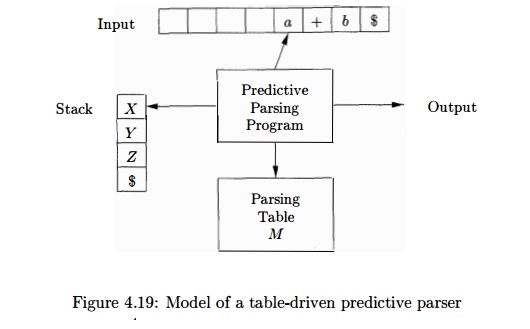
The table-driven parser in Fig. 4.19 has an input buffer, a stack containing a sequence of grammar symbols, a parsing table constructed by Algorithm 4.31, and an output stream. The input buffer contains the string to be parsed, followed by the endmarker $. We reuse the symbol $ to mark the bottom of the stack, which initially contains the start symbol of the grammar on top of $.

The parser is controlled by a program that considers X, the symbol on top of the stack, and a, the current input symbol. If X is a nonterminal, the parser chooses an X-production by consulting entry M[X, a] of the parsing table M. (Additional code could be executed here, for example, code to construct a node in a parse tree.) Otherwise, it checks for a match between the terminal X and current input symbol a.

The behavior of the parser can be described in terms of its configurations, which give the stack contents and the remaining input. The next algorithm describes how configurations are manipulated.

Algorithm 4 . 3 4 :  Table-driven predictive parsing.

INPUT : A string w and a parsing table M for grammar G.

OUTPUT : If w is in L(G), a leftmost derivation of w; otherwise, an error indication.

METHOD : Initially, the parser is in a configuration with w$ in the input buffer and the start symbol S of G on top of the stack, above $. The program in Fig. 4.20 uses the predictive parsing table M to produce a predictive parse for the input.

set ip to point to the first symbol of w;

set X to the top stack symbol; 

w h i le ( X $ ) { /* stack is not empty */

 if ( X is a ) pop the stack and advance ip;

 else if ( X is a terminal ) errorQ;

 else if ( M[X,a]  is an error entry ) errorQ;

 else if (  M[X,a]  = X -> Y1Y2   •••Yk) {

  output the production X -> Y1 Y2   • • • Yk;

  pop the stack; 

  push Yk, Yk-i,... ,Yi onto the stack, with Y1  on top;

}

set X to the top stack symbol;

}

Figure 4.20:  Predictive parsing algorithm

Example 4.35 : Consider grammar (4.28); we have already seen its the parsing table in Fig. 4.17. On input id + id * id, the nonrecursive predictive parser of Algorithm 4.34 makes the sequence of moves in Fig. 4.21. These moves correspond to a leftmost derivation (see Fig. 4.12 for the full derivation):

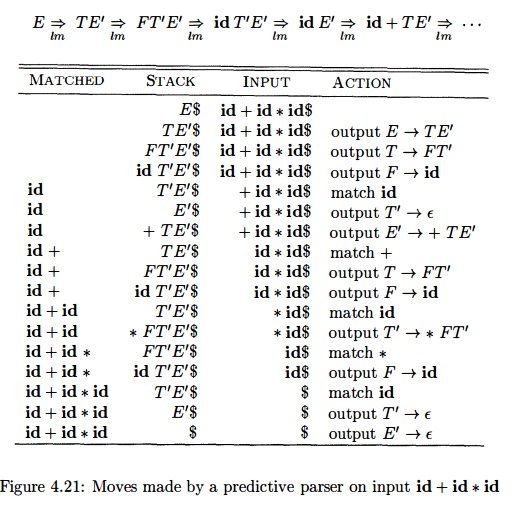
Note that the sentential forms in this derivation correspond to the input that has already been matched (in column M A T C H E D ) followed by the stack contents. The matched input is shown only to highlight the correspondence. For the same reason, the top of the stack is to the left; when we consider bottom-up parsing, it will be more natural to show the top of the stack to the right. The input pointer points to the leftmost symbol of the string in the INPUT column.

5. Error Recovery in Predictive Parsing

This discussion of error recovery refers to the stack of a table-driven predictive parser, since it makes explicit the terminals and nonterminals that the parser hopes to match with the remainder of the input; the techniques can also be used with recursive-descent parsing.

An error is detected during predictive parsing when the terminal on top of the stack does not match the next input symbol or when nonterminal A is on top of the stack, a is the next input symbol, and M[A, a] is error (i.e., the parsing-table entry is empty).

Panic Mode

Panic-mode error recovery is based on the idea of skipping symbols on the the input until a token in a selected set of synchronizing tokens appears. Its effectiveness depends on the choice of synchronizing set. The sets should be chosen so that the parser recovers quickly from errors that are likely to occur in practice. Some heuristics are as follows:

            As a starting point, place all symbols in FOLLOW(A) into the synchro-nizing set for nonterminal A. If we skip tokens until an element of FOLLOW(A) is seen and pop A from the stack, it is likely that parsing can continue.

            It is not enough to use FOLLOW(A) as the synchronizing set for A. For example, if semicolons terminate statements, as in C, then keywords that begin statements may not appear in the FOLLOW set of the nontermi-

nal representing expressions. A missing semicolon after an assignment may therefore result in the keyword beginning the next statement be-ing skipped. Often, there is a hierarchical structure on constructs in a language; for example, expressions appear within statements, which ap-pear within blocks, and so on. We can add to the synchronizing set of a lower-level construct the symbols that begin higher-level constructs. For example, we might add keywords that begin statements to the synchro-nizing sets for the nonterminals generating expressions.

3. If we add symbols in FIRST(A) to the synchronizing set for nonterminal

A, then it may be possible to resume parsing according to A if a symbol in FIRST (A) appears in the input.

            If a nonterminal can generate the empty string, then the production de-riving e can be used as a default. Doing so may postpone some error detection, but cannot cause an error to be missed. This approach reduces the number of nonterminals that have to be considered during error re-covery.

            If a terminal on top of the stack cannot be matched, a simple idea is to pop the terminal, issue a message saying that the terminal was inserted, and continue parsing. In effect, this approach takes the synchronizing set of a token to consist of all other tokens.

E x a m p l e 4 . 3 6 : Using FIRST and FOLLOW symbols as synchronizing tokens works reasonably well when expressions are parsed according to the usual gram-mar (4.28). The parsing table for this grammar in Fig. 4.17 is repeated in Fig. 4.22, with "synch" indicating synchronizing tokens obtained from the FOLLOW set of the nonterminal in question. The FOLLOW sets for the non-terminals are obtained from Example 4.30.

The table in Fig. 4.22 is to be used as follows. If the parser looks up entry M[A,a] and finds that it is blank, then the input symbol a is skipped. If the entry is "synch," then the nonterminal on top of the stack is popped in an attempt to resume parsing. If a token on top of the stack does not match the input symbol, then we pop the token from the stack, as mentioned above.

On the erroneous input ) id * + id, the parser and error recovery mechanism of Fig. 4.22 behave as in Fig. 4.23.

The above discussion of panic-mode recovery does not address the important issue of error messages. The compiler designer must supply informative error messages that not only describe the error, they must draw attention to where the error was discovered.

Phrase - level  Recovery

Phrase-level error recovery is implemented by filling in the blank entries  in the predictive parsing table with pointers to error routines. These routines may change, insert, or delete symbols on the input and issue appropriate error messages. They may also pop from the stack. Alteration of stack symbols or the pushing of new symbols onto the stack is questionable for several reasons. First, the steps carried out by the parser might then not correspond to the derivation of any word in the language at all. Second, we must ensure that there is no possibility of an infinite loop. Checking that any recovery action eventually results in an input symbol being consumed (or the stack being shortened if the end of the input has been reached) is a good way to protect against such loops.

6. Exercises for Section 4.4

Exercise 4 . 4 . 1 : For each of the following grammars, devise predictive parsers and show the parsing tables. You may left-factor and/of eliminate left-recursion from your grammars first.

            The grammar of Exercise 4.2.2(a).

            The grammar of Exercise 4.2.2(b).

            The grammar of Exercise 4.2.2(c).

            The grammar of Exercise 4.2.2(d).

            The grammar of Exercise 4.2.2(e).

            The grammar of Exercise 4.2.2(g).

        Exercise 4 . 4 . 2 : Is it possible, by modifying the grammar in any way, to con-struct a predictive parser for the language of Exercise 4.2.1 (postfix expressions with operand a)?

Exercise 4 . 4 . 3 : Compute FIRST and FOLLOW for the grammar of Exercise 4.2.1.

Exercise 4 . 4 . 4 : Compute FIRST and FOLLOW for each of the grammars of Exercise 4.2.2.

Exercise 4 . 4 . 5 : The grammar S -» a S a | a a generates all even-length strings of a's. We can devise a recursive-descent parser with backtrack for this grammar. If we choose to expand by production S ->• a a first, then we shall only recognize the string aa. Thus, any reasonable recursive-descent parser will try S -> a S a first.

a) Show that this recursive-descent parser recognizes inputs aa, aaaa, and aaaaaaaa, but not aaaaaa.

!! b)  What language does this recursive-descent parser recognize?

The following exercises are useful steps in the construction of a "Chomsky Normal Form" grammar from arbitrary grammars, as defined in Exercise 4.4.8.

! Exercise 4 . 4 . 6 :        A grammar is e-free if no production body is e  (called an

e-productiori).

            Give an algorithm to convert any grammar into an e-free grammar that generates the same language (with the possible exception of the empty string — no e-free grammar can generate e).

b) Apply your algorithm to the grammar S aSbS 1 bSaS | e. Hint: First find all the nonterminals that are nullable, meaning that they generate e, perhaps by a long derivation.

! Exercise 4 . 4 . 7: A single production is a production whose body is a single nonterminal, i.e., a production of the form A -> A.

            Give an algorithm to convert any grammar into an e-free grammar, with no single productions, that generates the same language (with the possible exception of the empty string) Hint: First eliminate e-productions, and then find for which pairs of nonterminals A and B does A =4» B by a sequence of single productions.

            Apply your algorithm to the grammar (4.1) in Section 4.1.2.

c) Show that, as a consequence of part (a), we can convert a grammar into an equivalent grammar that has no cycles (derivations of one or more steps in which A ^ A for some nonterminal A).

 Exercise 4 . 4 . 8: A grammar is said to be in Chomsky Normal Form (CNF) if every production is either of the form A ->• BC or of the form A ->• a, where A, B, and C are nonterminals, and a is a terminal. Show how to convert any grammar into a CNF grammar for the same language (with the possible exception of the empty string — no CNF grammar can generate e).

 Exercise 4 . 4 . 9 : Every language that has a context-free grammar can be recognized in at most 0 ( n 3 ) time for strings of length n. A simple way to do so, called the Cocke-Younger-Kasami (or CYK) algorithm is based on dynamic programming. That is, given a string axa2 • • • a„, we construct an n-by-n table T such that Tij is the set of nonterminals that generate the substring a{ai+1 •••aj.

If the underlying grammar is in CNF (see Exercise 4.4.8), then one table entry can be filled in in O(n) time, provided we fill the entries in the proper order: lowest value ofj-i first. Write an algorithm that correctly fills in the entries of the table, and show that your algorithm takes 0 ( n 3 ) time. Having filled in the table, how do you determine whether a1 a2 • • • an is in the language?

Exercise 4.4.10: Show how, having filled in the table as in Exercise 4.4.9, we can in 0(n) time recover a parse tree for a1a2---an. Hint: modify the table so it records, for each nonterminal A in each table entry Tij: some pair of nonterminals in other table entries that justified putting A in Tij.

Exercise 4.4.11 : Modify your algorithm of Exercise 4.4.9 so that it will find, for any string, the smallest number of insert, delete, and mutate errors (each error a single character) needed to turn the string into a string in the language of the underlying grammar.

Exercise 4 . 4 . 1 2 :  In Fig. 4.24 is a grammar for certain statements.  You may take e and s to be terminals standing for conditional expressions and  "other statements," respectively. If we resolve the conflict regarding expansion of the optional "else" (nonterminal stmtTail) by preferring to consume an else from the input whenever we see one, we can build a predictive parser for this grammar. Using the idea of synchronizing symbols described in Section 4.4.5:

 Build an error-correcting predictive parsing table for the grammar.

 Show the behavior of your parser on the following inputs:

(i) if e then s ; if e then s end

( M ) while e do begin s ; if e then s ; end